一、 奥卡姆剃刀(Occam's razor)原理:
在所有可能选择的模型中,我们应选择能够很好的解释数据,并且十分简单的模型。从贝叶斯的角度来看,正则项对应于模型的先验概率。可以假设复杂模型有较小的先验概率,简单模型有较大的先验概率。
二、正则化项
2.1、什么是正则化?
正则化是结构风险最小化策略的实现,在经验风险上加一个正则项或罚项,正则项一共有两种L1正则化和L2正则化,或者L1范数和L2范数。对于线性回归模型,使用L1正则化的模型叫做Lasso回归;使用L2正则化的模型叫做Ridge回归(岭回归)
2.2、正则化项和模型复杂度之间的关系
正则化项一般是模型复杂度的单调递增的函数,模型越复杂,正则化值越大。
一般来说,监督学习可以看做最小化下面的目标函数:
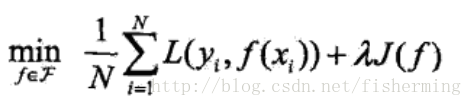
上式中的第1项为经验风险,即模型f(x)关于训练数据集的平均损失;第2项为正则化项,去约束我们的模型更加简单
三、L1范数
3.1 概念: L1范数是指向量中各个元素绝对值之和。
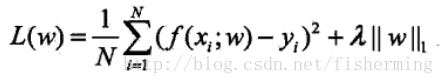
3.2 为什么L1范数会使权值稀疏?
任何的正则化算子,如果他在Wi=0的地方不可微,并且可以分解为“求和” 的形式,那么这个正则化算子就可以实现稀疏。
3.3 参数稀疏有什么好处?
(1)特征选择(Feature Selection)
参数稀疏规则化能够实现特征的自动选择,在特征工程的过程中,一般来说,xi的大部分元素(特征)都和其标签yi没有关系的。我们在最小化目标函数的时候,考虑了这些无关特征,虽然可以获得最小的训练误差,但是对于新的样本时,这些没用的信息反而被考虑,干扰了对样本的预测。稀疏规则化将这些没用的特征的权重置为0,去掉这些没用的特征。
(2)可解释性
将无关特征置为0,模型更容易解释。例如:患某种病的概率为y,我们收集到的数据x是1000维的,我们的任务是寻找这1000种因素是如何影响患上这种病的概率。假设,我们有一个回归模型:y=w1*x1+w2*x2+…+w1000*x1000+b,通过学习,我们最后学习到w*只有很少的非零元素。例如只有5个非零的w*,那么这5个w*含有患上这种病的关键信息。也就是说,是否患上这种病和这5个特征相关,那事情变得容易处理多了。
四、L2范数
4.1 概念:L2范数是指向量各元素的平方和然后再求平方根。
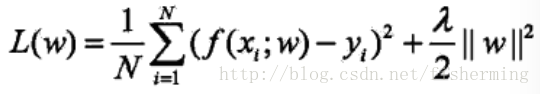
正则化项可以取不同的形式。对于回归问题中,损失函数是平方损失,正则化项为参数向量L2的范数。
4.2 为什么L2范数可以防止过拟合?
左一:欠拟合;中间:正常拟合;右侧:过拟合
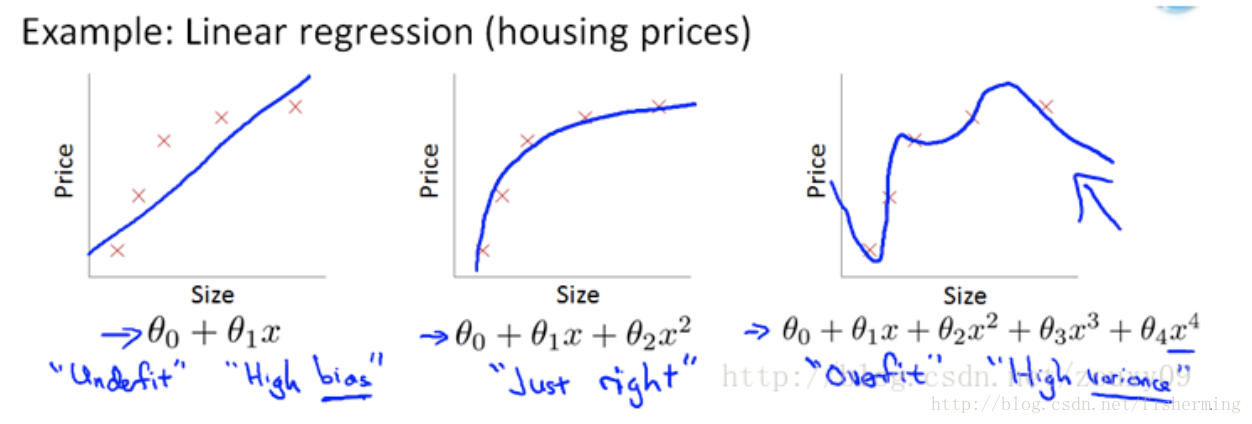
让L2范数的正则项||W||2最小,可以使得W的每个元素都很小,都接近于0。(L1范数让W等于0),而越小的参数说明模型越简单,越简单的模型越不容易产生过拟合的现象。(结合上图线性回归拟合图可知,限制了某些参数很小,其实也就限制了多项式的某些分量的影响很小,这也就相当于减少了变量的个数)
版权声明:本文为CSDN博主「baidu-liuming」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/fisherming/article/details/79492602