图像卷积概念
图像卷积操作(convolution),或称为核操作(kernel),是进行图像处理的一种常用手段,
图像卷积操作的目的是利用像素点和其邻域像素之前的空间关系,通过加权求和的操作,实现模糊(blurring),锐化(sharpening),边缘检测(edge detection)等功能。
图像卷积的计算过程就是卷积核按步长对图像局部像素块进行加权求和的过程。
卷积核实质上是一个固定大小的权重数组,该数组中的锚点通常位于中心。
卷积核大小
通常情况下,选取卷积核大小为1x1,3x3,5x5,7x7等
取奇数大小的目的是为了设置卷积核中心为锚点,方便卷积核和图像的对齐处理
设置卷积核大小对称的目的是为了在空间域中充分利用像素点和其领域像素间的关系。当然这不是必须的,如果需要针对某一轴进行处理,可以设置1x3或3x1大小。
参考:
Convolution
Kernel (image processing)
图像卷积数学公式
二维离散卷积公式如下:
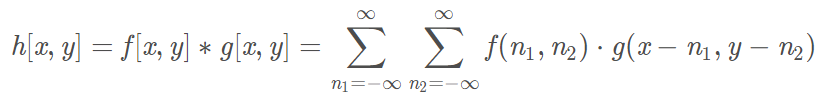
图像卷积通常使用这个公式,其中g[x,y]g[x,y]g[x,y]为卷积核,符号∗\ast∗表示卷积操作
图形化表示
以一维离散卷积公式为例:

其图形化公式如下:
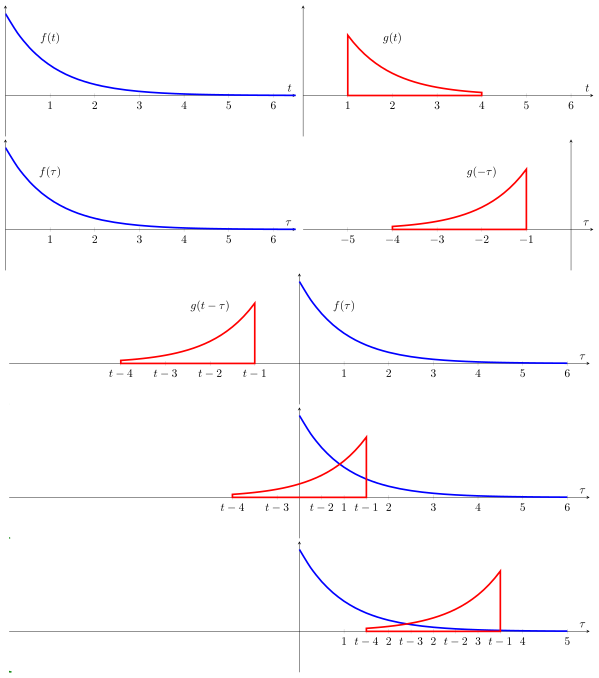
- 首先将函数 g(τ) 反射为 g(−τ) ,相当于 g(τ) 沿yyy轴翻转
- 再对函数 g(−τ) 添加一个时间偏移量 t ,它允许函数 g(t−τ) 沿着 τ 轴移动
- 变量 t 每增加 1,表示函数 g(t−τ) 向左移动一步
- 计算 t 遍历 −∞ 到 ∞ 的过程中,函数 f(τ) 和 g(t−τ) 的重叠面积
举例
函数 f = [1,2,3,4] ,函数 g = [1,3,2]
将函数 g 逆转:g(τ) ⇒ g(−τ),值变为[2,3,1]
计算过程如下:
h(0)=[1]⋅[1]=1⋅1=1
h(1)=[1,2]⋅[3,1]=1⋅3+2⋅1=3+2=5
h(2)=[1,2,3]⋅[2,3,1]=1⋅2+2⋅3+3⋅1=2+6+3=11
h(3)=[2,3,4]⋅[2,3,1]=2⋅2+3⋅3+4⋅1=4+9+4=17
h(4)=[3,4]⋅[2,3]=3⋅2+4⋅3=6+12=18
h(5)=[4]⋅[2]=4⋅2=8
h(x)=[1,5,11,17,18,8]
以此类推可知二维离散卷积的计算过程,先对角翻转卷积核,在逐步向两个正方向移动,计算重叠面积
- flip the mask (horizontally and vertically) only once(水平和垂直翻转掩模一次)
- slide the mask onto the image(在图像上滑动掩模)
- multiply the corresponding elements and then add them(将相应的元素相乘,然后求和)
- repeat this procedure until all values of the image has been calculated(重复这一过程,直到所有图像值均已被计算)
多说一句,关于信号与系统中的LTI(linear time-invariant systems,线性时不变系统)和LSI(linear shift invariant system,线性位移不变系统)的不变性一直没太理解,图形化理解就是信号(函数)可以随着时间/空间移动而不改变它的原先的形状,就像卷积核一样。
图像卷积注意事项
在进行卷积操作时,需要注意两点
卷积核归一化
卷积核的大小和值可以根据要求定义,但通常会将整个卷积核进行归一化操作,其目的是为了保证修改后结果图像的平均元素值和原始图像平均元素值一样。
因为卷积操作满足齐次性,所以可以卷积计算完成后再除以整个卷积核的值。
数值精度
图像数值类型通常为uint8,在进行卷积操作时很容易造成数值溢出,所以在进行操作之前可以先转换成更高精度的数值类型
版权声明:本文为CSDN博主「编号1993」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/u012005313/article/details/84068337
