浅析深度学习之卷积

1、什么是卷积

卷积神经网络顾名思义，是一种使用了卷积运算的神经网络。随着深度学习技术的发展，卷积神经网络的复杂度不断提升，逐渐发展出针对不同问题而设计的卷积（convolution）运算。从数学上理解，卷积一种特殊的线性运算，但它具有很重要的物理意义，并且在很多领域中得到了应用。例如统计学中，加权滑动平均是一种卷积；概率论中，两个统计独立变量X与Y和的概率密度函数是X与Y的概率密度函数的卷积；信号处理中，傅里叶变换将时域信号转换成频域也是采用的卷积。

在传统的图像处理中，线性滤波过程的本质就是卷积运算，图1演示了一个在二维图像上进行卷积运算的过程。卷积核的概念并不神秘，如图1中所示，它就是一个2x2的矩阵。然而，不同的卷积核作用也大不相同。通过使用卷积核进行卷积运算，我们可以从输入图像中提取某些相关的“特征”。卷积运算则是在图像上，采用卷积核与输入进行滑动相乘并求和，如图1所示，输出的图像中每个像素值，是输入图像中的一个2x2的矩阵块与核对应位置相乘然后求和所得。

图1 卷积示例

为什么说通过卷积运算可以提取图像中的某些特征呢？我们举个小例子来看一下，图2显示了一个3x3的卷积核，经过该卷积核的卷积运算，可以看到输出图像的“轮廓”更加明显了。这是因为该卷积核使得：

输出图像上的像素点的值=该像素点的原始值值+该像素点与周围像素点差值

从而可知，当某个像素点周围像素与其相差越大时，这个像素点的值变化就越大，而图像中不同物体之间相邻的边界处像素点的变化值较大，因此经过卷积运算后，输出图像会让人觉得图像中物体的轮廓更加明显了。

图2 卷积操作示例

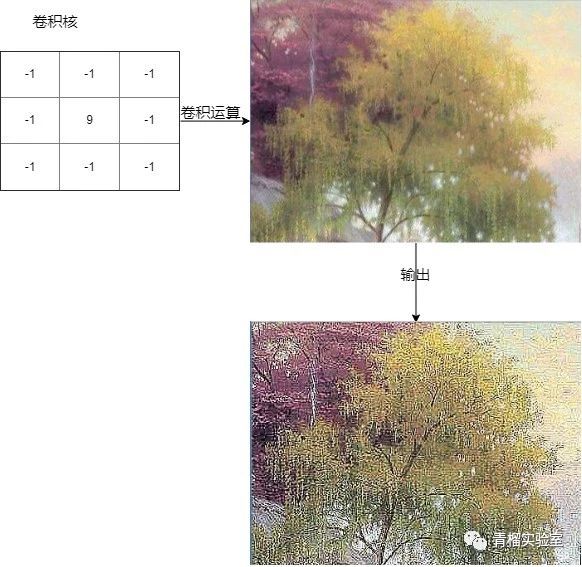
图2中的卷积核可以通过提取边缘特征，从而使得图像“锐化”。那么，通过改变卷积核内的参数的值，我们可以得到更多有意义的卷积核。在卷积神经网络中，给定输入数据，通过优化这些参数和卷积的方法等，从而提取关键特征，使得期望网络输出结果接近目标输出结果。

为了进一步了解卷积运算，下面介绍一些卷积中常用的概念：

1）卷积核的大小（Kernel Size）定义了卷积的大小范围，常见的卷积核的尺寸有1x1、2x2、3x3等等，图1中卷积核的大小为2x2，图2中的大小为3x3；

2）步长（Stride）定义了当卷积核在图像上面进行卷积操作的时候，每次卷积运算跨越的像素点的个数；

3）填充（Padding）：从图1可以看到，经过卷积运算输出图像的尺寸会缩小，填充就是在图像外围补充一些像素，使得输入输出的尺寸保持一致；

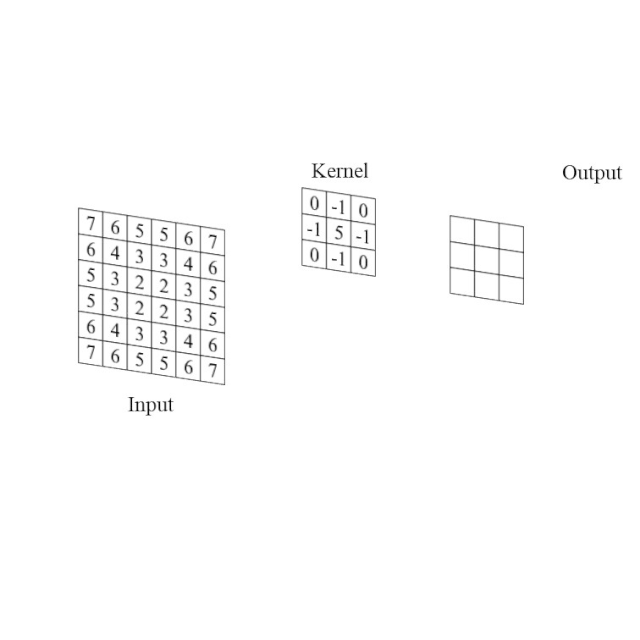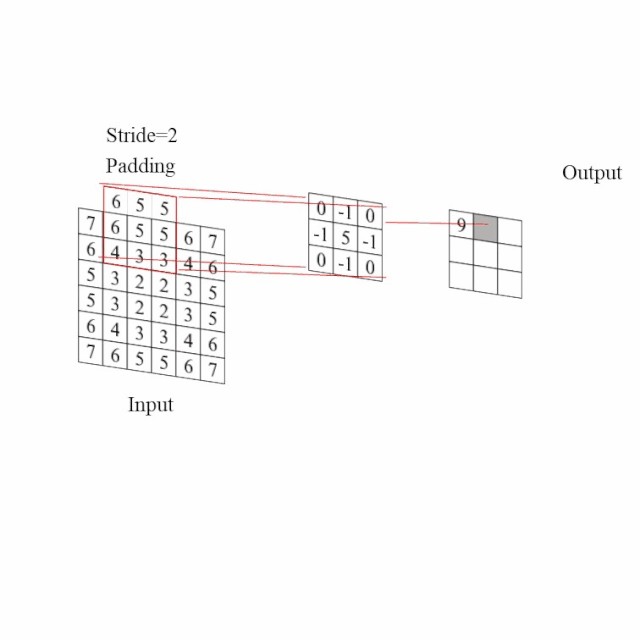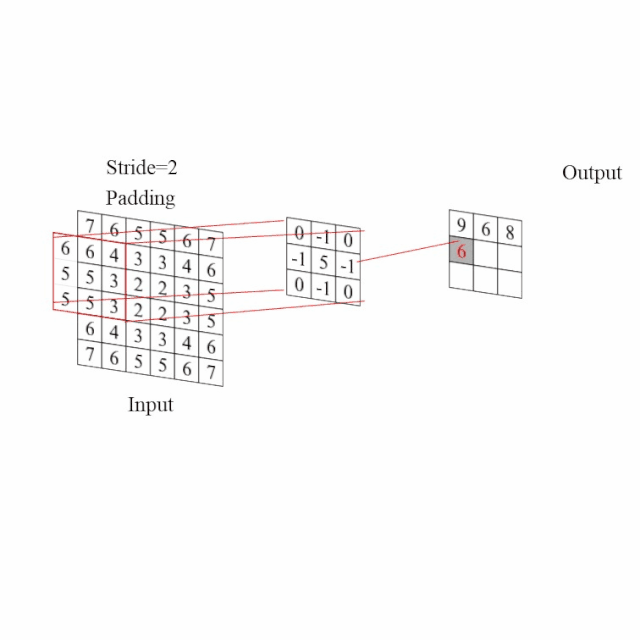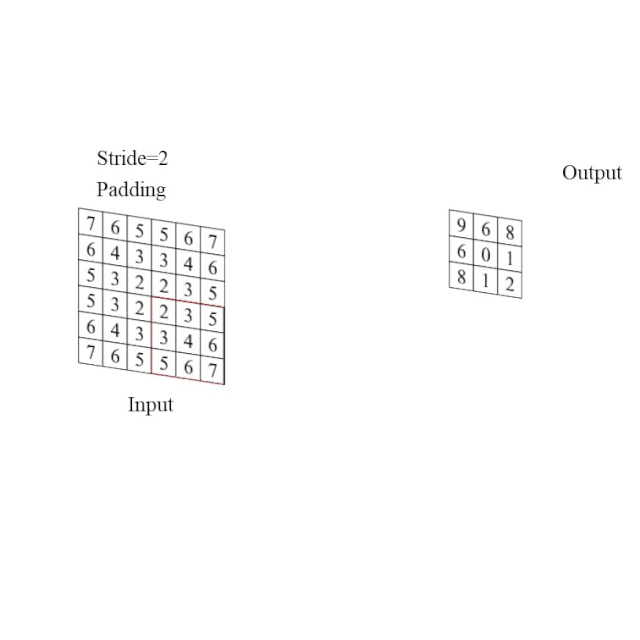
图3给出了填充=1、步长=2、卷积核为3x3的卷积过程。根据卷积尺寸、大小、填充等的变化可以划分为不同的类型，而这些类型各有其特点，并且在不同的网络中发挥不同的作用。

下面我们一起看看都有哪些各具特色的卷积吧。

2、卷积的种类及应用

二维卷积：二维卷积是最为常见的卷积，在机器视觉中大量使用，用于图像分割、图像识别、物体检测等等。我们在上一章已经给大家介绍过了单通道的2维卷积。对于输入是RGB的3通道图像，假设尺寸为m*n*3，卷积核会对每个通道的图像进行卷积，然后再将卷积后输出的3张m*n图像(加padding)对应像素点求和，最终得到一个m*n的输出特征；如果我们的卷积核有k个，那么经过这些卷积核的输出特征的尺寸为m*n*k。

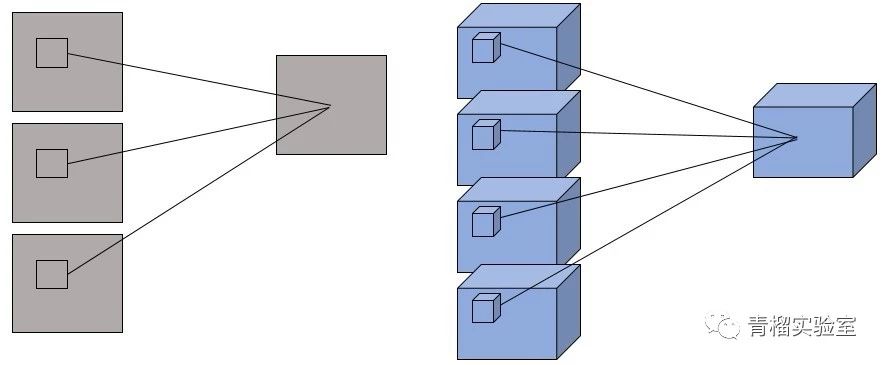
三维卷积：二维卷积可以作用于图像，用于提取图像在空域中的特征信息。但是对于视频，二维卷积无法获取时间维度上的信息。因此很容易想到，可以把二维卷积扩展到三维，用于同时捕捉视频的时域以及空域的信息。相比于图像，视频还多了一维时间信息。由于3维卷积作用于4维（长x宽x通道x时间）的数据，难以进行可视化，下图以单通道的数据为例，可以对比出二维和三维卷积的差别。

图4 二维与三维卷积

1x1卷积：卷积核大小为1x1的卷积，可以通过控制卷积核的个数，改变输出特征的维度，通常用于降维/升维。由于1x1的卷积可以在保持输出特征与输入保持一致的（即不损失分辨率）前提下，利用其后接的非线性激活函数可以大大增加网络的非线性特征，从而提升网络的拟合能力。我们所熟知的GoogLeNet中就引入了大量的1x1卷积。

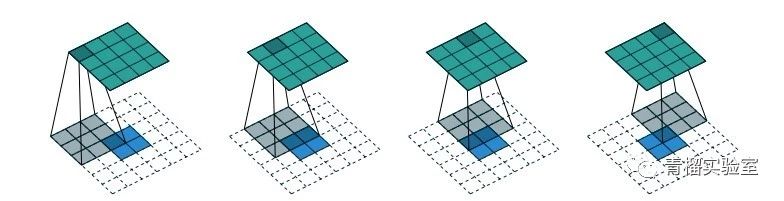
转置(Transposed)卷积：对转置卷积的需求通常来自于使用与普通卷积相反方向的转换。图5给出了一个转置卷积的示例，输入尺寸为2x2，经过3x3的卷积操作，得到输出尺寸为4x4。可以看到，转置卷积并不是卷积的逆运算，而一种特殊的正向卷积，即先按照一定的比例通过补0来扩大输入图像的尺寸，接着再进行正向卷积，从而可以实现将低维特征映射映射到高维空间，如实现常见的上采样等。

图5 转置卷积^[1]

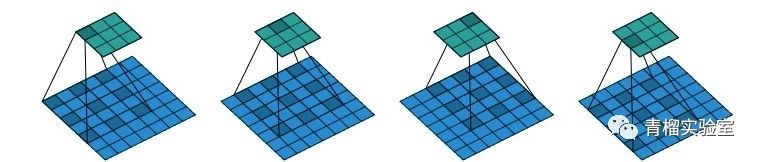
空洞卷积：是在经典卷积基础上调整得到的，空洞卷积同时完成卷积的特征提取与池化层的特征压缩，采用的思路很是巧妙：在更大的范围用小卷积核做卷积。以二维的3x3卷积为例，经典卷积就在原图像上提取3x3的区域与3x3的卷积核作卷积。空洞卷积则是在原图像上提取5x5的区域，然后选择3x3个像素，与3x3的卷积核作卷积。这样单次卷积计算仍是3x3卷积计算量，但采样范围扩大到了5x5，在较大的范围内同时实现了特征提取与特征压缩，基本上无需添加额外的成本就能有较大的感受野。下图展示了一次空洞卷积的计算过程。空洞卷积由于较小的计算量和优异的性能，现广泛应用到各个需要精细化分割的图像任务中。

图6 空洞卷积^[1]

3、小结

卷积是深度卷积网络中最基础最重要的组成单元，直到今天还有很多科学家在研究新的卷积形式。我们只介绍了卷积家族中的一小部分，还有更多有趣的卷积和网络结构，等待着大家去挖掘和探索。

4、参考文献

[1]Vincent Dumoulin, Francesco Visin
A guide toconvolution arithmetic for deep learning (BibTeX)
[2] https://github.com/vdumoulin/conv_
arithmetic

本文转自：青榴实验室，转载此文目的在于传递更多信息，版权归原作者所有。
作者：赵璐