现如今,卷积神经网络在人工智能领域应用的广泛性及重要性可谓是不言而喻。为了让大家对卷积的类型有一个清晰明了的认识,可以快速概述不同类型的卷积及其好处。在这里绘制了动图,以方便大家的学习(仅关注二维卷积)。
卷积(Convolutions)
首先,我们需要就定义卷积层的几个参数。
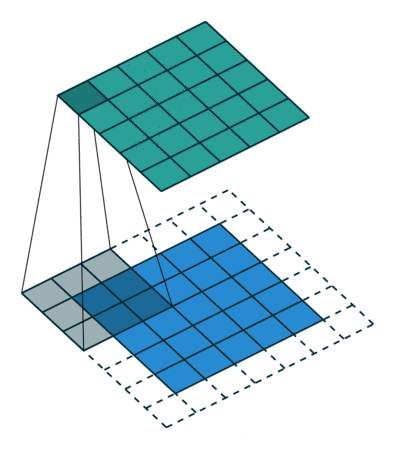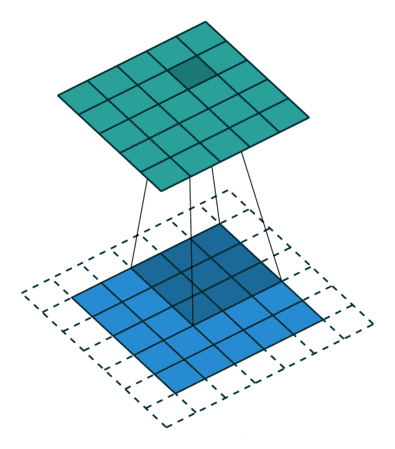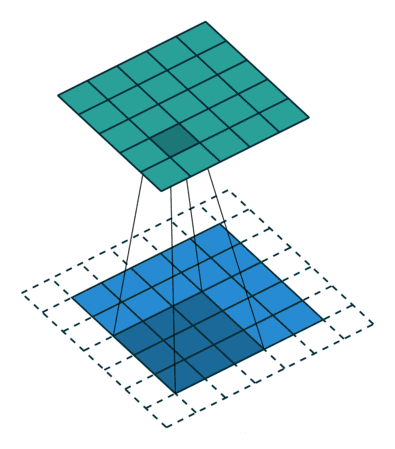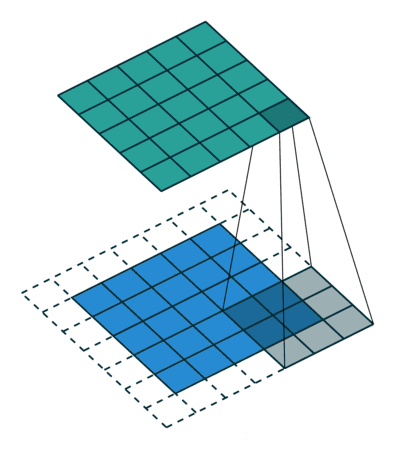
内核大小:内核大小定义了卷积的视野。二维的常见选择是3——即3x3像素。
步幅:步幅定义了遍历图像时内核的步长。虽然它的默认值通常为1,但我们可以使用2的步长,类似于最大池化对图像进行下采样。
padding:padding定义样本的边框如何处理。一(半)个padding卷积将保持空间输出尺寸等于输入尺寸,而如果内核大于1,则不加卷积将消除一些边界。
输入和输出通道:卷积层需要一定数量的输入通道(I),并计算出特定数量的输出通道(O)。可以通过I * O * K来计算这样一层所需的参数,其中K等于内核中的值的数量。
扩张卷积(Dilated Convolutions)
(又名阿鲁斯卷积)
扩张卷积引入另一个卷积层的参数被称为扩张率。这定义了内核中值之间的间距。扩张速率为2的3x3内核将具有与5x5内核相同的视野,而只使用9个参数。想象一下,使用5x5内核并删除每个间隔的行和列。
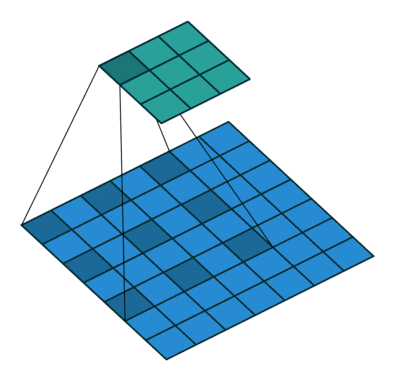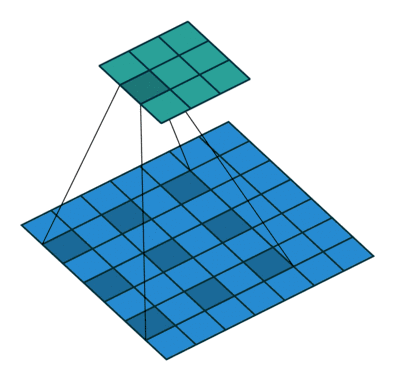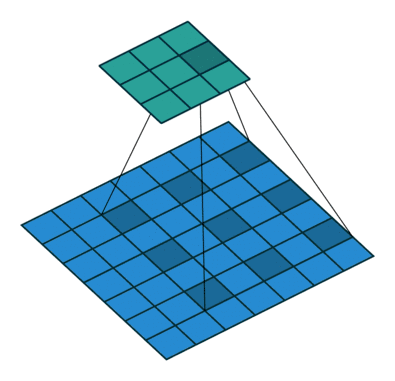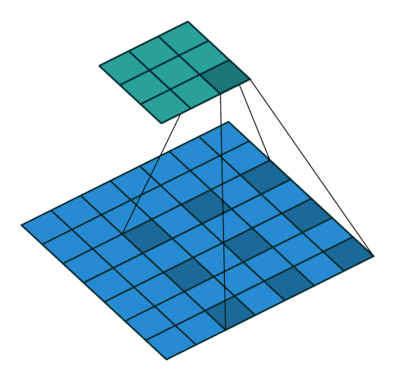
它使得系统能够以相同的计算成本提供更广泛的观察范围。扩张卷积在实时分割领域特别受欢迎。如果你需要更大的观察范围,且无法承受多个卷积或更大的内核,请考虑使用它。
转置卷积(Transposed Convolutions)
(又名反卷积或分段缠绕卷积)
一些人使用反卷积这个名称,这不是特别恰当的,因为它不是一个反卷积。使事情变得更糟糕的反卷积确实存在,但在深度学习领域并不常见。实际的反卷积是反转卷积的过程。想象一下,将图像输入到单个卷积层。现在开始输出,把放置到一个黑盒子里,然后将你的原始图像再次输出。这个黑盒子进行了一个反卷积操作。这就是卷积层的数学反演。
转置的卷积在某种程度上来说是相似的,因为它和一个假设的反卷积层所产生的空间分辨率是相同的。但是,正在执行的实际数学运算在值上是不同的。转置卷积层执行的是常规卷积,但它会恢复其空间变换。
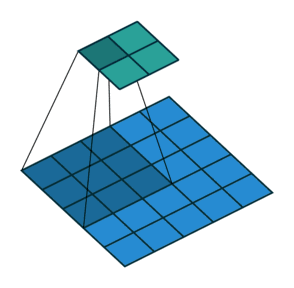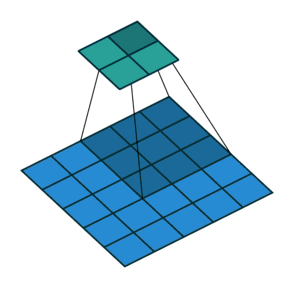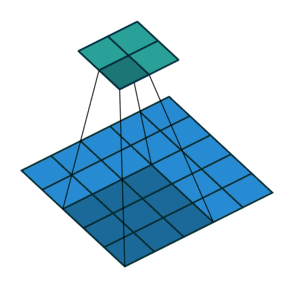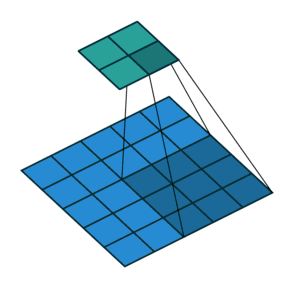
关于这一点你可能会感到困惑,所以让我们来看一个具体的示例。将一个5x5的图像馈送到卷积层。其步幅设置为2,padding禁用,内核为3x3。结果是产生一个2x2的图像。
如果我们想反转这个过程,我们需要反数学运算,以便从我们输入的每个像素中生成9个值。之后,我们以2步幅的设置来遍历输出图像。这将是一个反卷积。

而转置卷积将不会进行此类操作。唯一的共同之处在于它保证输出也将是一个5x5的图像,同时仍然执行正常的卷积运算。为了实现这一点,我们需要在输入上执行一些漂亮的padding。
正如你现在可以想象的,这一步并不会从上面扭转这个过程。至少不包括数值。
它只是在以往的基础上重建空间分辨率并执行卷积操作。这可能不是数学的反演,但是对于Encoder-Decoder架构来说,它仍然非常有用。这样,我们可以将图像的缩放与卷积相结合,而不是将两个过程单独分开进行。
可分离卷积(Separable Convolutions)
在一个可分离卷积中,我们可以将内核操作拆分成多个步骤。我们用y = conv(x,k)表示卷积,其中y是输出图像,x是输入图像,k是内核。这一步很简单。接下来,我们假设k可以由下面这个等式计算得出:k = k1.dot(k2)。这将使它成为一个可分离的卷积,因为我们可以通过对k1和k2做2个一维卷积来取得相同的结果,而不是用k做二维卷积。
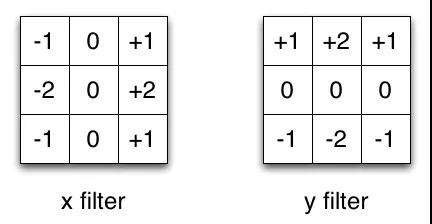
我们以通常用于图像处理的Sobel内核为例。你可以通过乘以向量[1,0,-1]和[1,2,1] .T获得相同的内核。在执行相同的操作时,你只需要6个而不是9个参数。
上面的示例显示了所谓的空间可分离卷积,据我所知,这并不是在深度学习中使用的。我只是想确保在他人费劲地操作时,你不会受到如此困惑。在神经网络中,我们通常使用的是一种叫做深度可分离卷积的神经网络。
这将执行一个空间卷积,同时保持通道独立,然后进行深度卷积操作。在我看来,为了加深了解,可以用一个示例作为典范。
假设我们在一个16输入通道和32输出通道上有一个3x3的卷积层。那么将要发生的就是16个通道中的每一个都由32个3x3的内核进行遍历,从而产生512(16x32)的特征映射。接下来,我们通过将每个输入通道中的特征映射相加从而合成一个大的特征映射。由于我们可以进行此操作32次,因此我们得到了期望的32个输出通道。
那么,针对同一个示例,深度可分离卷积的表现又是怎样的呢?我们遍历16个通道,每一个都有一个3x3的内核,可以给出16个特征映射。现在,在做任何合并操作之前,我们将遍历这16个特征映射,每个都含有32个1x1的卷积,然后才逐此开始添加。这导致与上述4608(16x32x3x3)个参数相反的656(16x3x3 + 16x32x1x1)个参数。
该示例是深度可分离卷积的具体实现,其中所谓的深度乘数为1。而这是目前为止这些层最常见的设置。
我们这样做是因为假设空间和深度信息是可以去耦的。而反观Xception模型的表现,可以发现这个理论似乎是有效的。其实,可移动设备中也可以使用深度可分离卷积。因为它们的参数是可以有效利用的。
总结
到此为止,可以说对于卷积网络类型的介绍就要告一段落了。我希望能帮助大家简要了解一下这个问题。而接下来,我们将为大家展示一些卷积动画,帮助大家对此做深一步了解。
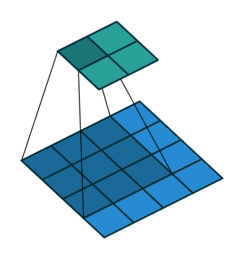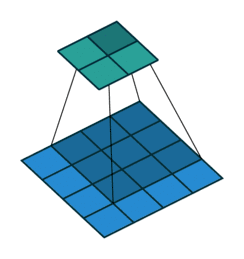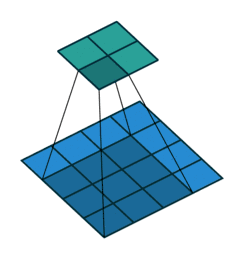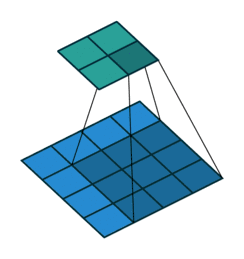
01 无padding无步幅

02 随机padding无步幅
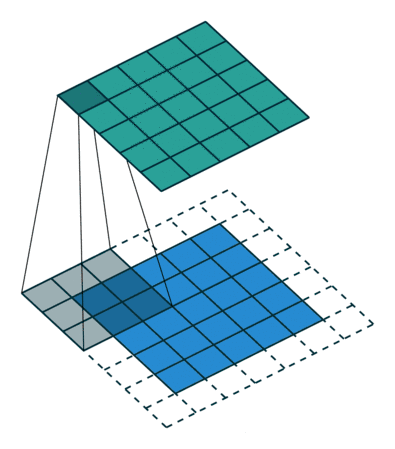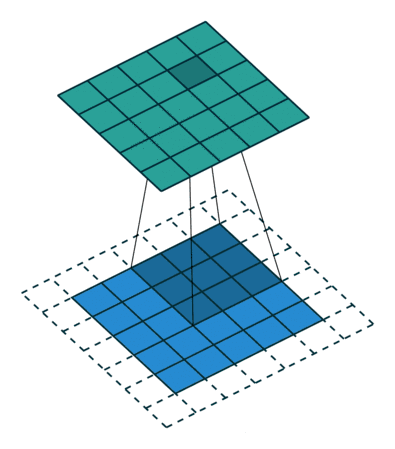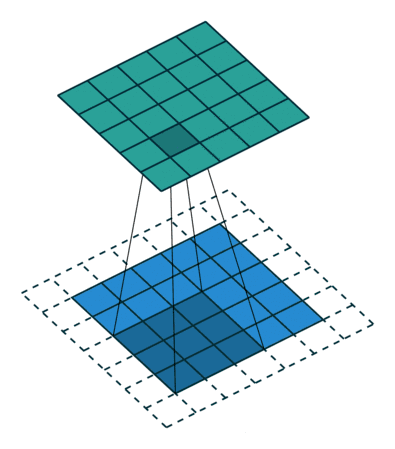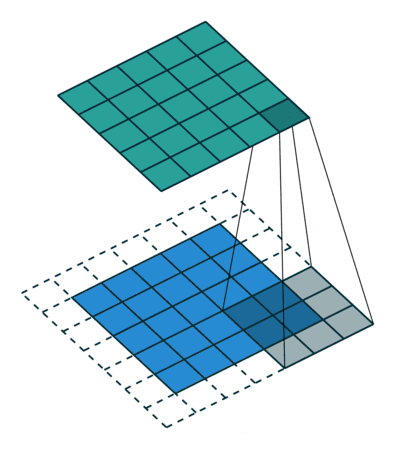
03 半padding无步幅
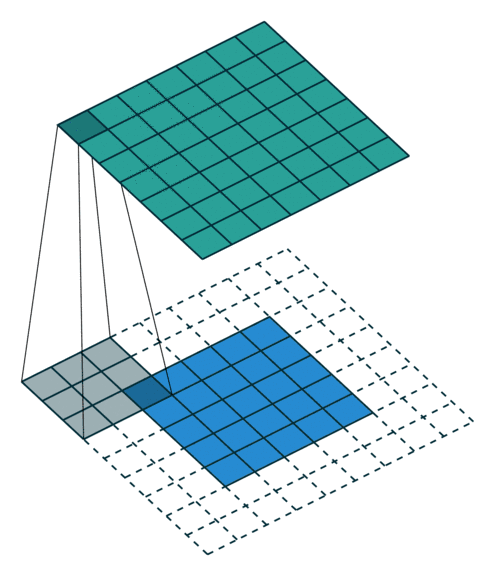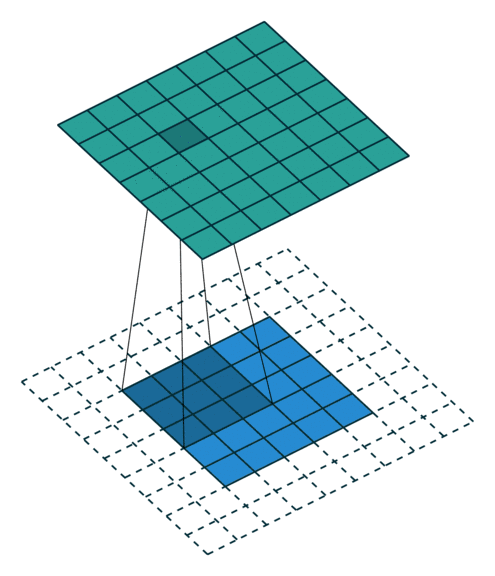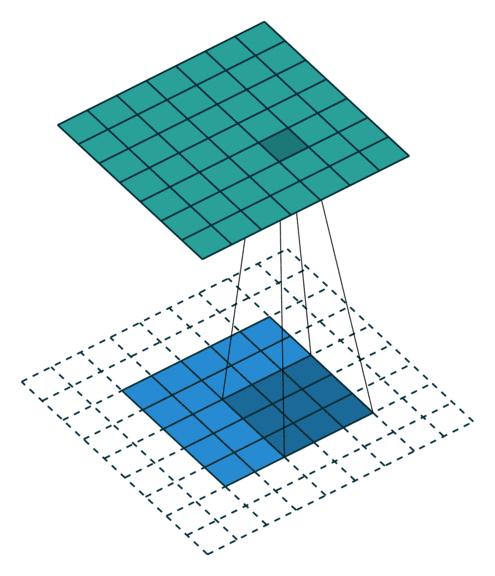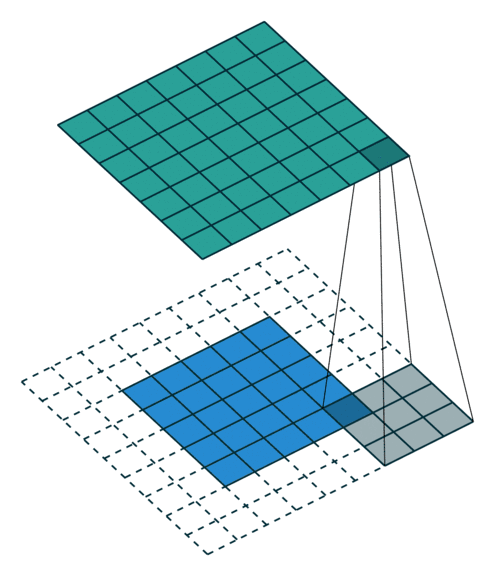
04 全padding无步幅
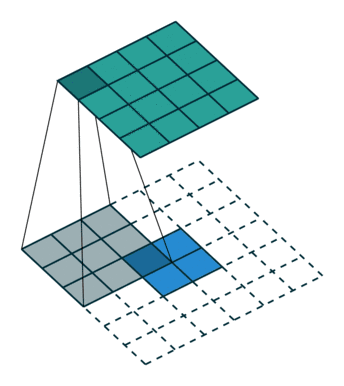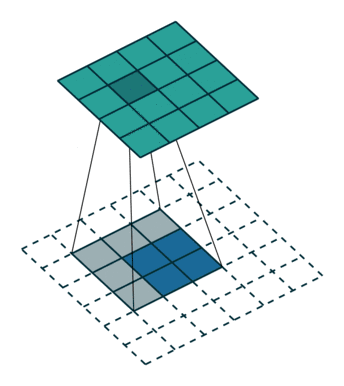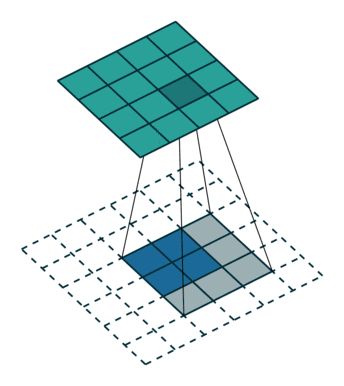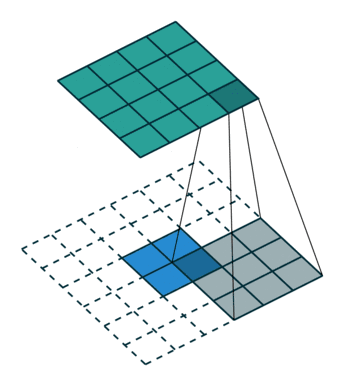
05 无padding无步幅转置

06 随机padding无步幅转置

07 半padding无步幅转置
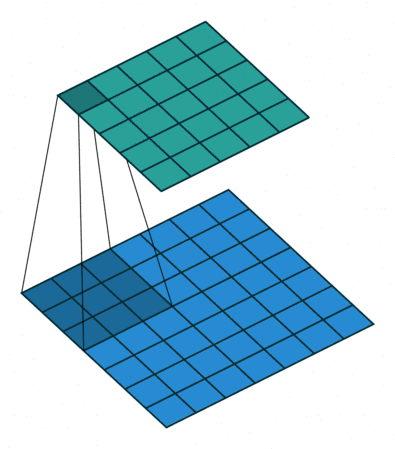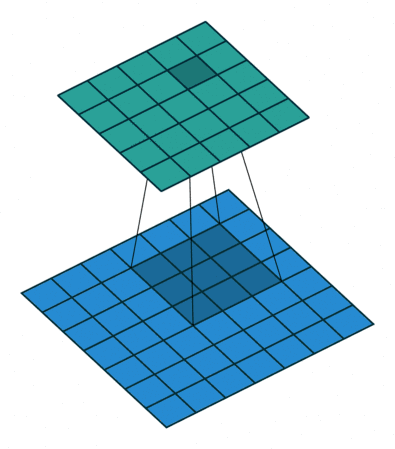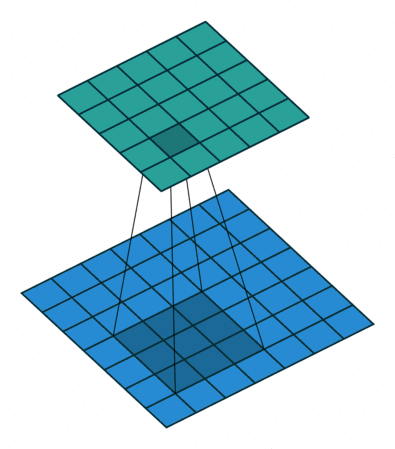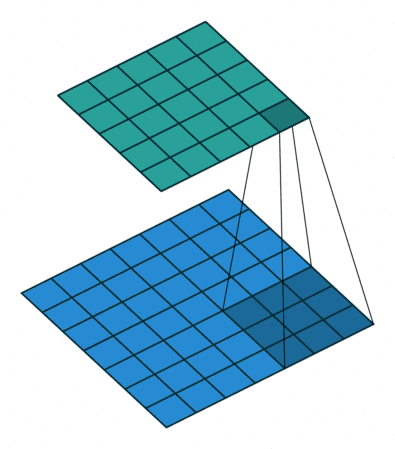
08 全padding无步幅转置
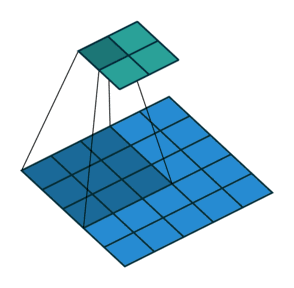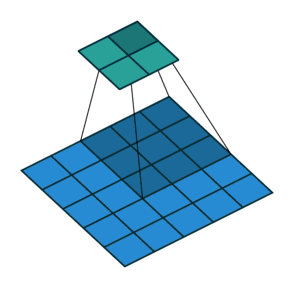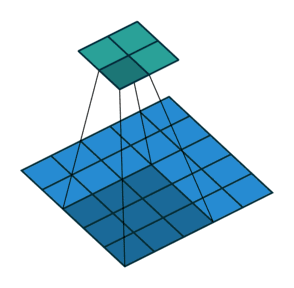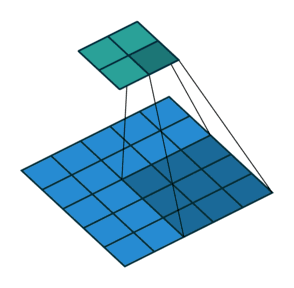
09 无padding有步幅
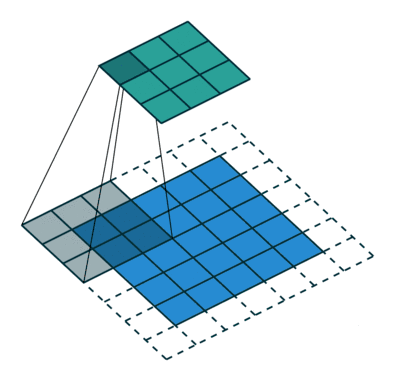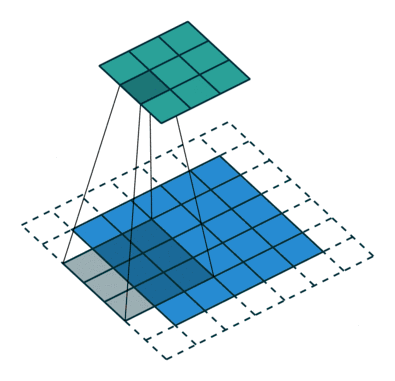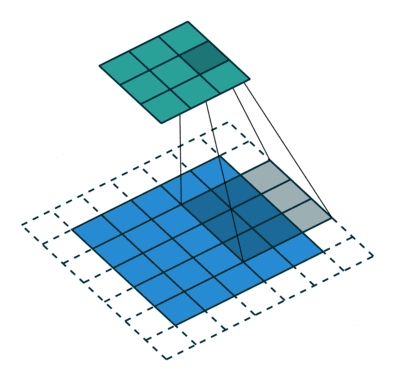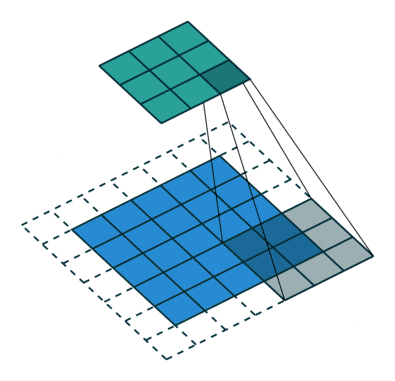
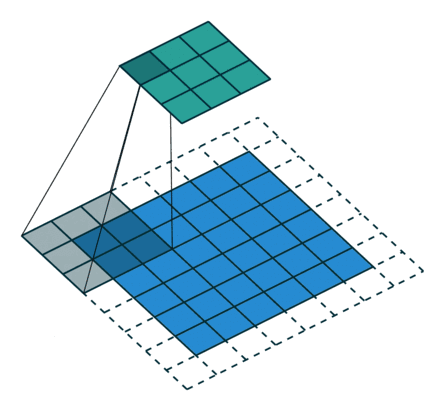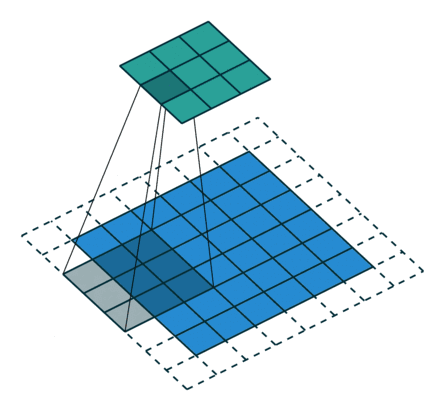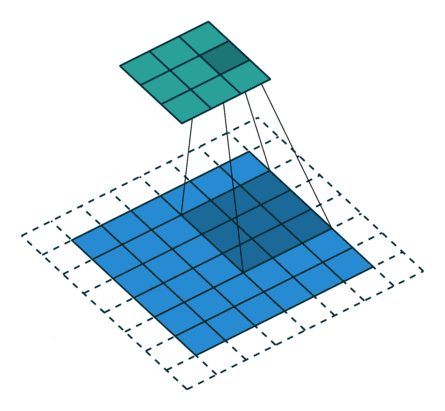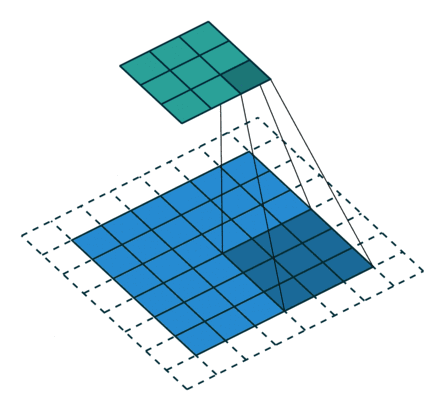
10 有padding有步幅
11 有padding有步幅(奇数)
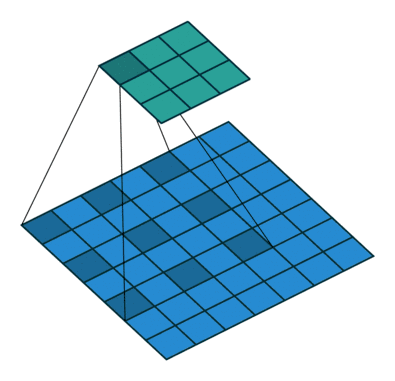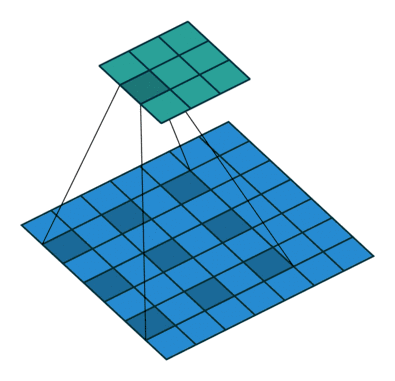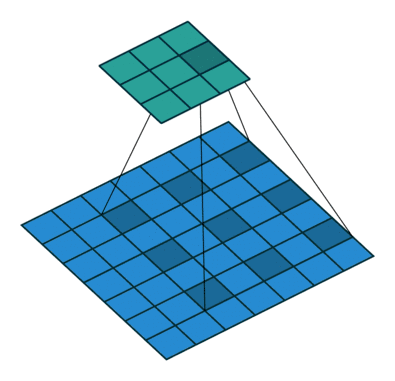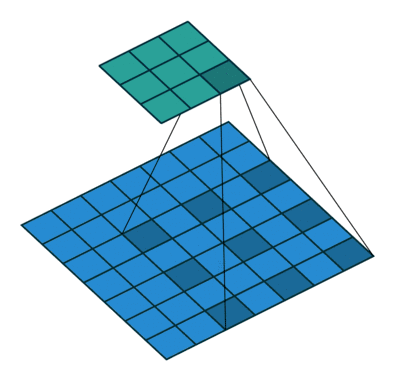
12 扩张
本文转自: LSGO软件技术团队,转载此文目的在于传递更多信息,版权归原作者所有。