本篇博客主要是基于花书(古德费洛的《Deep Learning》)和西瓜书(周志华的《机器学习》)撰写的,其中插入了博主的一些个人见解,如有不对之处希望大家指出来一起来讨论一下嘿嘿,万分感谢。
什么是一个好的机器学习算法?
我想我们可以先从这个问题开始:一个机器学习算法满足什么条件才能被称得上是一个好算法?
机器学习的主要挑战是我们的算法必须能够在先前未观测到的新输入上表现良好,而不只是在训练集上表现良好。这个很容易理解,因为我们平时里所做的就是给一个机器学习算法喂一大堆数据(训练集),然后希望这个算法在新数据(测试集)上有良好的性能。而这种在先前未观测到的输入上表现良好的能力被称为泛化能力。
为了得到泛化能力好的学习器,我们应该从训练样本中尽可能学出适用于所有潜在样本的“普遍规律”,这样才能在遇到新样本时做出正确的判别。如果我们把训练样本的一些特有的特点也当做潜在样本的一般性质,这样就会导致泛化能力下降,这也是我们常说的“过拟合”现象。
与“过拟合”相对的是“欠拟合”,即训练样本的性质都没有学习完全,这样又怎么能指望对未知的新样本表现良好呢?举个例子,比如现在要识别猫和狗。猫和狗都有两个眼睛,有四肢,有尾巴,有毛发,如果我们学习器学习能力不行,只学习到了这些比较“浅”的特征,那么这个学习器肯定都无法对训练集图片进行正确的分类,这就是欠拟合。如果学习器不仅学习到了这些特征,还学习到了猫和狗有不同的体型、体态、眼睛形状等合理的特征,那么我们不仅在训练集上分类误差很低,在测试集上也能达到不错的效果,这是学习器成功的例子。如果再进一步,学习器在之前的基础上,还学到了很多不必要的特征,比如训练集中有的狗少了一只腿,或者黄色毛发的狗比较多,那么学习器很有可能将一只少了一条腿的猫分类到狗的类别,或者认为其他颜色毛发的狗是狗的概率很低。这些特征强烈干扰了学习器的正确判断,这便是“过拟合”。
总结一下,决定机器学习算法效果是否好有如下两个因素:
(1) 降低训练误差
(2) 缩小训练误差和测试误差的差距
这两个因素分别对应机器学习的两个挑战:欠拟合和过拟合。欠拟合是指模型不能在训练集上获得足够低的误差,而过拟合是指训练误差和测试误差之间的差距太大。
独立同分布假设
上面提到我们希望尽可能最小化模型的泛化误差,那么泛化误差应该如何衡量呢?通常我们是通过度量在训练集中划分出来的测试集样本上的性能,来近似估计模型的泛化误差。但归根到底,测试集也是我们“能观测到的已有的数据”的一部分,用它来代表剩下的未观察到的潜在数据还是具有太大的局限性。不过,我们也不能为了识别猫狗,就把世界上所有的猫狗照片全部找过来,我们能够分别猫狗,但我们也没有见过世界上所有的猫狗,不是吗?
对于这个问题统计学理论提供了一些答案。现在不妨换个角度思考,假设我们现在得到了世界上所有的猫狗照片的数据,但是因为太多,我们还是不想全部使用,于是我们按照一定规律从中抽取一些数据,保证这些数据包含所有的必要特征,能够100%代表整体数据。在这样的假设下,训练集误差、测试集误差以及剩下所有数据的误差理论上应该都一样,这不正是我们想要的效果?
现在将上面的大白话说的更理论化一些。训练集和测试集数据通过数据集上被称为数据生成过程的概率分布生成,我们假设每个数据集中的样本都彼此相互独立,并且训练集和测试集都是同分布的,采样自相同的分布,我们将这个共享的潜在分布称为数据生成分布,记为 pdata 。这就是独立同分布假设,这使得我们能够用单个样本的概率分布表述数据生成过程。
在独立同分布的假设下,训练样本的误差就等价于潜在样本的误差,我们只要尽可能降低训练误差即可。但实际上这个假设基本不能能成立,我们往往只是利用部分数据预测整个数据分布,从这个角度来说“过拟合”是无法彻底避免的,我们所能做只是缓解或者减小其风险。幸运的是,但这并不影响我们使用这个假设,大多数情况下算法还是能得到比较令人满意的结果,而且我们还可以使用其他技巧进一步提升结果。
模型容量与过拟合
现在再从模型容量的角度谈一谈过拟合。
模型的容量是指其拟合各种函数的能力。我们可以将一个模型视为一个复杂的函数 f(X) = Y ,给定输入 X ,然后就能得到相应的输出 Y 。这个函数参数越多,函数就越复杂,能够拟合的函数也就越多越高级。当然,影响模型容量的不止是参数数量,训练目标也能影响。训练模型的目的就是从这些函数中挑选出最优函数,然而实际中算法不会真的找到最优函数,而仅是找到一个可以大大降低训练误差的函数。一些额外的限制因素,比如优化算法的不完美,会导致算法容量减小。
通过调整模型的容量,我们可以控制模型是否偏向于过拟合或欠拟合。当机器学习算法的容量适合于所执行任务的复杂度和所提供训练数据的数量时,算法效果通常会最佳。容量不足的模型不能解决复杂任务;容量高的模型能够解决复杂的任务,但是当其容量高于任务所需时,有可能会发成生拟合。如下图所示。

我们比较了线性、二次和9次函数拟合真实二次函数的效果。线性函数无法刻画真实函数的曲率,所以欠拟合。9次函数能够表示正确的函数,但因为训练参数比样本还多,所以它也能表示无限多个刚好穿过训练样本点的其他函数,我们很难从这些不同解中选出一个泛化良好的。二次模型非常符合任务的真实结构,因此它可以很好地泛化到新数据上。
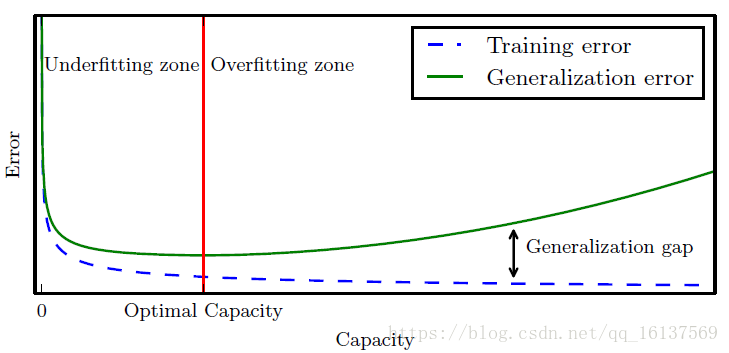
上图是容量和误差之间的典型关系。在达到最优容量前,训练误差和泛化误差都很高(容量不够时,最优函数可能没有包括在模型能够拟合的函数族中)。如果继续增加容量,训练误差减小,但是训练误差和泛化误差的间距不断扩大,最终这个间距超过训练误差的下降,进入到过拟合机制。因此我们不能为了降低训练误差一味提高模型容量,要针对具体问题选择合适的模型容量。
最后再来看看训练样本数量对模型有什么影响。
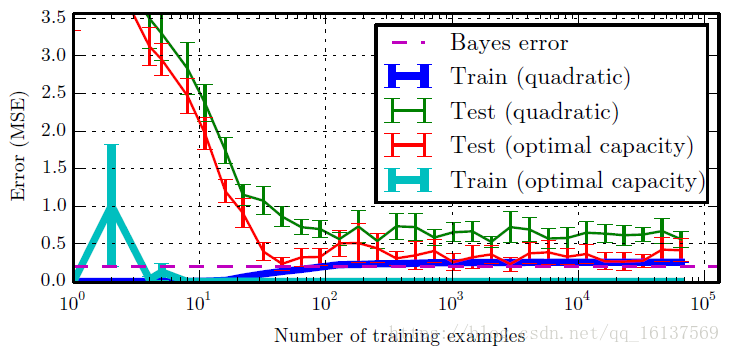
举个栗子,通过给一个5阶多项式添加适当的噪声,构造一个回归问题,然后用二次模型和最优容量的模型去求解该问题,如上图所示。图中紫色的虚线是贝叶斯误差,即从预先知道的真实分布预测而出现的误差,也是理论上能达到的最佳误差。比如说,一个骰子,理论上6个面出现的概率都是1616,但如果我们实际扔6次,并不能保证每个面各出现一次,这个误差就叫做贝叶斯误差(也可以理解为系统固有误差?)。总之一个算法因为各种各样的原因肯定会有误差,而贝叶斯误差就是一个算法能达到的最优误差。
对于二次模型,当训练样本数量还不足以匹配其模型容量时,训练误差会随着样本的增加而降低,但如果继续增加训练样本,超过了模型的拟合能力,训练误差(图中蓝色的线)会开始上升。而测试误差会随之减小,这是因为训练数据越多,关于训练数据的不正确的假设就越少。由于二次模型的容量不足以解决该问题,所以测试误差会稳定在一个较高的水平。
对于最优容量的模型,测试误差最终会趋近于贝叶斯误差。训练集误差可以低于贝叶斯误差,因为该模型有能力记住训练集中的样本。但当训练集趋于无穷大时,任何固定容量的模型的训练误差都至少增至贝叶斯误差。
有心的人可能会问,误差既能被模型容量影响又能被样本数量影响,那么我们该如何针对某个容量的模型选择训练集大小,或者已有某个大小的训练集,如何选择合适容量的模型呢?
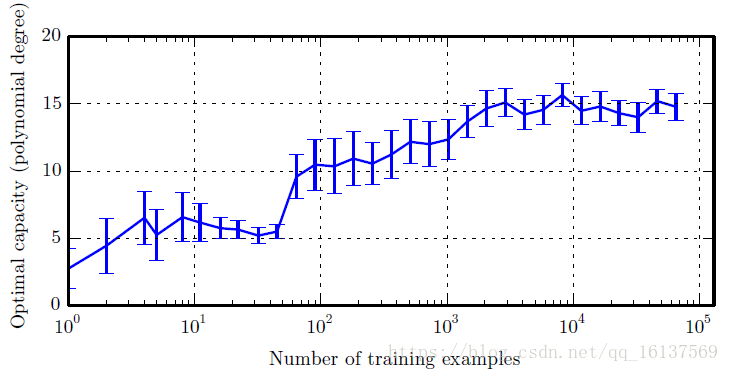
从上面这张图解释了这个问题。可以看到,当训练集增大时,最优容量也会随之增大,但当最优容量足够捕获模型复杂度之后就不再增长了。
到这里可能还是有点绕,结论还没那么清晰。现在将两张图结合在一起看一下,现在我们假定要解决的问题的复杂度是固定的。当样本数量不够多时,训练集还不能很好的反应真实的数据分布pdatapdata,即用小训练集学习到的只是全部数据的部分特征,每次增加训练集都引入了新的有用特征,模型发现现有模型容量不足以学习,所以在初期模型的最优容量会随着训练集的增大而增大。如果训练集增加到一定地步,这时训练集已经足够反应真实数据分布了,再增加训练集只是相当于多了一些重复的样本,所以模型的最优容量不会再增加了。在这个增加训练集大小的过程中,如果在中途因为训练样本不够中止了,这个训练集大小对应的模型最优容量小于问题的复杂度,那么此时测试误差就会偏高,因为这个容量下无法捕获到真实数据分布的全部信息。
在实际应用中,我们通常是用有限的数据去预测真实分布。如果我们选择刚好和这个训练集大小相匹配的模型容量,往往测试误差会偏高,因为此时的模型容量和问题复杂度不匹配。而且模型容量是一个很模糊的边界,很难确定一个深度学习算法的容量,所以通常我们会使用一个容量比训练集大很多的模型,来避免容量不够的问题,但这样岂不是会发生过拟合?是的,但通过正则化等方法我们可以减轻过拟合带来的影响。正则化将在下一篇博客中讲。
总结
本来打算将过拟合和正则化放到同一篇博客里的,结果发现过拟合讲了这么多(知识真是常读常新啊)。
回到正题,在我看来,过拟合的表象是训练误差很小,而测试误差很大,给人一种模型“记住”样本的感觉,所以换个新样本就瓦特了。但归根到底还是模型容量以及训练集这两者和问题复杂度是否匹配的问题。
如果模型容量过小,无论你给多少训练样本,都无法得到一个较低水平的泛化误差,还有可能发生欠拟合;
如果模型容量超过问题的复杂度,但你给的训练样本不够(不是指数量,而是其包含的特征不够),模型很轻松能学习到训练集的特征,但泛化能力依旧很有限,这就导致了过拟合;
只有当模型容量和训练集大小这两者与问题复杂度平衡时,才能得到理想的泛化误差。
不过现实中条件有限,无法得知数据的真实分布,所以通常使用大容量模型+正则化来得到不错的结果。
版权声明:本文为CSDN博主「Maples丶丶」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_16137569/article/details/81504853






