L1正则为什么更容易获得稀疏解？

L1和L2正则常被用来解决过拟合问题。而L1正则也常被用来进行特征选择，主要原因在于L1正则化会使得较多的参数为0，从而产生稀疏解，将0对应的特征遗弃，进而用来选择特征。

但为什么L1正则会产生稀疏解呢？这里利用公式进行解释。

假设只有一个参数为 w，损失函数为L(w)，分别加上L1正则项和L2正则项后有：

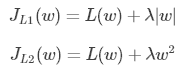
假设L(w)在0处的倒数为 d₀ ，即

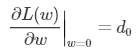
则可以推导使用L1正则和L2正则时的导数。

引入L2正则项，在 0 处的导数

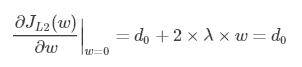
引入L1正则项，在0处的导数

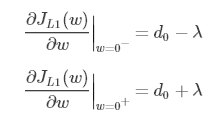
可见，引入L2正则时，代价函数在 0 处的导数仍是 d₀ ，无变化。而引入L1正则后，代价函数在0处的导数有一个突变。从 d₀ + λ 到 d₀ − λ ，若 d₀ + λ 和 d₀ − λ 异号，则在 0 处会是一个极小值点。因此，优化时，很可能优化到该极小值点上，即 w = 0 处。

这里只解释了有一个参数的情况，如果有更多的参数，也是类似的。因此，用L1正则更容易产生稀疏解。

版权声明：本文为CSDN博主「keep_forward」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/b876144622/article/details/81276818