作者:Manas Sahni
编译:ronghuaiyang
来源:AI公园(ID:AI_Paradise)
在我不太破旧的笔记本电脑CPU上,使用TensorFlow这样的库,我可以(最多)在10-100毫秒内运行大多数常见的CNN模型。在2019年,即使是智能手机也能在不到半秒的时间内运行“重”CNN(比如ResNet)模型。所以,想象一下当给我自己的卷积层的简单实现计时的时候,我很惊讶,发现它为一个单层花费了2秒!
现代深度学习库对大多数操作都具有生产级的、高度优化的实现,这并不奇怪。但这些库究竟是什么魔法?他们如何能够将性能提高100倍?究竟怎样才能“优化”或加速神经网络的运行呢?在讨论高性能/高效DNNs时,我经常会问(也经常被问到)这些问题。
在这篇文章中,我将尝试带你了解在DNN库中卷积层是如何实现的。它不仅是在模型中最常见的和最重的操作,我还发现卷积高性能实现的技巧特别具有代表性——一点点算法的小聪明,非常多的仔细的调优和低层架构的开发。
我在这里介绍的很多内容都来自Goto等人的开创性论文:Anatomy of a high-performance matrix multiplication,该论文为OpenBLAS等线性代数库中使用的算法奠定了基础。
最原始的卷积实现
“过早的优化是万恶之源”——Donald Knuth
在进行优化之前,我们先了解一下基线和瓶颈。这是一个朴素的numpy/for循环卷积:
'''
Convolve `input` with `kernel` to generate `output`
input.shape = [input_channels, input_height, input_width]
kernel.shape = [num_filters, input_channels, kernel_height, kernel_width]
output.shape = [num_filters, output_height, output_width]
'''
for filter in 0..num_filters
for channel in 0..input_channels
for out_h in 0..output_height
for out_w in 0..output_width
for k_h in 0..kernel_height
for k_w in 0..kernel_width
output[filter, channel, out_h, out_h] +=
kernel[filter, channel, k_h, k_w] *
input[channel, out_h + k_h, out_w + k_w]这是一个6层嵌套的for循环(如果你迭代多个输入批次,则为7个)。我们还没有研究步幅,膨胀,或其他参数。如果我在这里输入MobileNet的第一层的大小,然后用普通的C语言运行它,它会花费惊人的22秒!使用最积极的编译器优化,如' -O3 '或' -Ofast ',它减少到2.2秒。但这对于第一层来说仍然非常慢。
如果我使用Caffe运行相同的层呢?这台电脑只用了18毫秒。这比100倍的加速还要快!整个网络在我的CPU上运行大约100毫秒。
瓶颈是什么,我们应该从哪里开始优化?
最内部的循环执行两个浮点运算(乘法和加法),对于我使用的大小,它执行了大约8516万次,也就是说,这个卷积需要1.7亿个浮点运算(MFLOPs)。根据英特尔的数据,我的CPU的最高性能是每秒800亿次,也就是说,理论上它可以在0.002秒内完成这项工作。显然,我们离这个目标还很远,而且很明显,这里的原始处理能力已经足够了。
理论峰值没有达到(从来没有)的原因是内存访问也需要时间—如果不能快速获得数据,那么仅仅快速处理数据是不够的。事实证明,上面嵌套的for循环使得数据访问模式非常困难,这使得缓存利用率很低。
正如你将看到的,在整个讨论过程中反复出现的一个问题是,我们如何访问正在操作的数据,以及这些数据如何与存储方式相关联。
一些先决条件
FLOP/s
我们对“性能”或速度的度量是吞吐量,以每秒浮点计算次数度量。具有更多浮点操作的更大操作自然会运行得更慢,因此FLOP/s速率可以使用更一致的方式来比较性能。
我们也可以用它来了解我们离CPU的最高性能有多近。
在我的笔记本电脑CPU上:
- 有2个phsyical core
- 每个核的频率为2.5 GHz,即每秒2.5×109个CPU周期
- 在每个周期,它可以处理32FLOPs(使用AVX和FMA还会更多)
其峰值性能为 GFLOP/s。这是我的CPU的理论峰值。同样,对于单个内核,这个数字是80GFLOP/s。
存储顺序和行主序
虽然我们从逻辑上把矩阵/图像/张量看作多维的,但它们实际上存储在线性的一维计算机内存中。我们必须定义一个约定,该约定规定如何将这些多维数据展开到线性存储中,反之亦然。
大多数现代DL库使用行主序存储。这意味着同一行的连续元素彼此相邻存储。更一般地说,对于多维,行主序意味着当线性扫描内存时,第一个维度的变化最慢。
那么维度本身的顺序呢?通常对于四维张量,比如CNNs,你会听到NCHW, NHWC等存储顺序。我将在这篇文章中假设NCHW——如果我有N块HxW图像的C通道,那么所有具有相同N个通道的图像都是重叠的,在该块中,同一通道C的所有像素都是重叠的,以此类推。
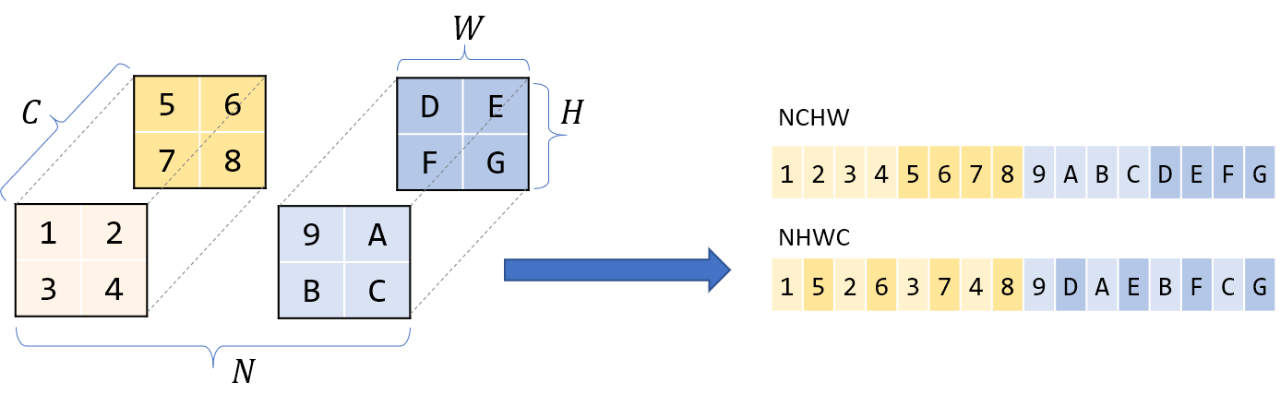
Halide
这里讨论的许多优化都需要在底层使用神秘的C语法,甚至是程序集进行干预。这不仅使代码难以阅读,还使尝试不同的优化变得困难,因为我们必须重新编写整个代码。Halide是c++中的一种嵌入式语言,它帮助抽象这些概念,并被设计用来帮助编写快速图像处理代码。通过分解算法(要计算什么)和计划(如何/何时计算),可以更容易地试验不同的优化。我们可以保持算法不变,并使用不同的策略。
我将使用Halide来表示这些较低级别的概念,但是你应该能够理解足够直观的函数名,以便理解。
从卷积到GEMM
我们上面讨论的简单卷积已经很慢了,一个更实际的实现只会因为步长、膨胀、填充等参数而变得更加复杂。我们可以继续使用基本的卷积作为一个工作示例,但是,正如你看到的,从计算机中提取最大性能需要许多技巧—在多个层次上进行仔细的微调并充分利用现有计算机体系结构的非常具体的知识。换句话说,如果我们希望解决所有的复杂性,这将是一项艰巨的任务。
我们能不能把它转化成一个更容易解决的问题?也许矩阵乘法?
矩阵乘法,或matmul,或Generalized Matrix Multiplication (GEMM)是深度学习的核心。它用于全连接层、RNNs等,也可用于实现卷积。
毕竟,卷积是带有输入padding的滤波器的点积。如果我们把滤波器放到一个二维矩阵中,把输入的小patch放到另一个矩阵中,然后把这两个矩阵相乘,就会得到相同的点积。与CNNs不同,矩阵乘法在过去几十年里得到了大量的研究和优化,在许多科学领域都是一个关键问题。
上面将图像块放到一个矩阵中的操作称为im2col ,用于图像到列。我们将图像重新排列成矩阵的列,使每一列对应一个应用卷积滤波器的patch。
考虑这个普通的,直接的3x3卷积:
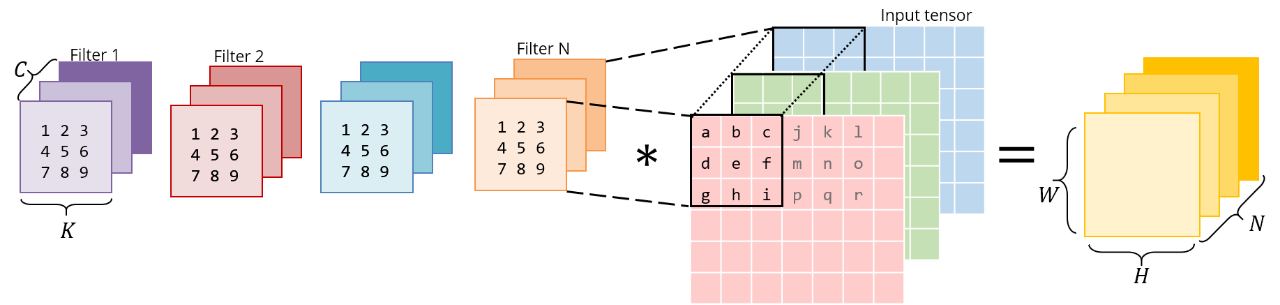
下面是与矩阵乘法相同的操作。正确的矩阵是im2col的结果——它必须通过复制原始图像中的像素来构造。左边的矩阵有conv权值,它们已经以这种方式存储在内存中。
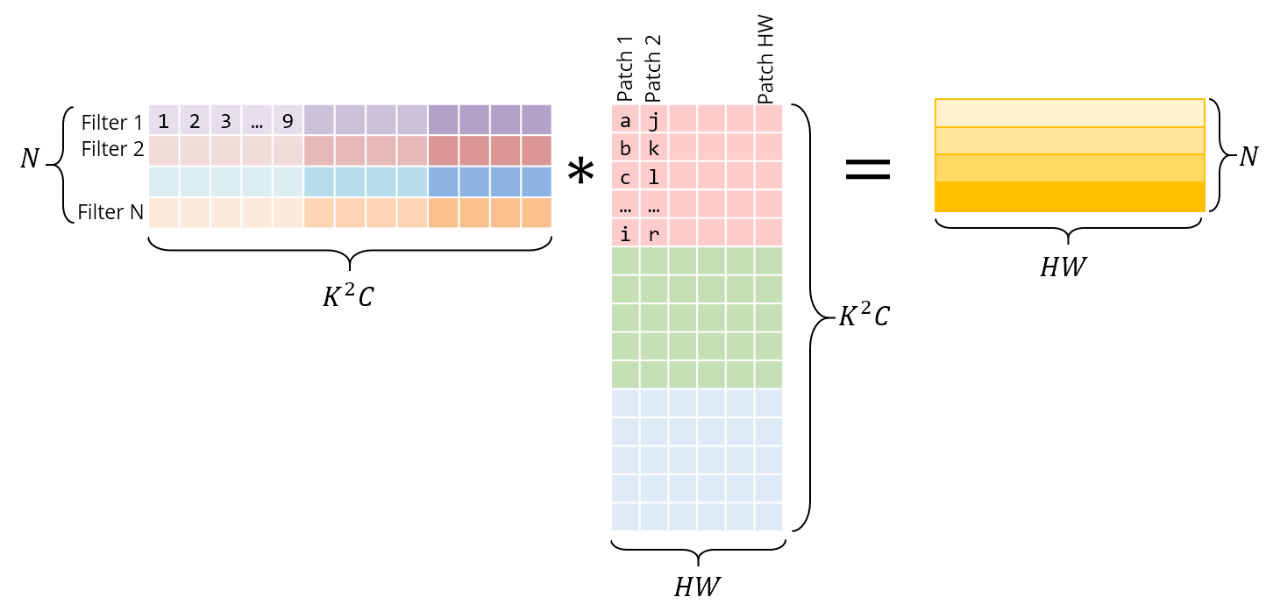
注意,矩阵乘积直接给出了conv输出——不需要额外的“转换”到原始形式。
为了清晰起见,我将每个patch都单独显示在这里。然而,在现实中,不同的图像块之间往往存在一定的重叠,因此im2col会产生一定的内存重复。生成这个im2col缓冲区和膨胀的内存所花费的时间,必须通过GEMM实现的加速来抵消。
利用im2col,我们已经将卷积运算转化为矩阵乘法。我们现在可以插入更多通用的和流行的线性代数库,如OpenBLAS、Eigen等,利用几十年的优化和仔细的调优,有效地计算这个matmul。
如果我们要证明im2col转换所带来的额外工作和内存是合理的,那么我们需要一些非常严重的加速,所以让我们看看这些库是如何实现这一点的。这也很好地介绍了在系统级进行优化时的一些通用方法。
虽然以前有过不同形式的convolution-as-GEMM思想,但Caffe是第一个在CPU和GPU上对通用convs使用这种方法的深度学习库之一,并显示了较大的加速。这里:https://github.com/yangqing//wiki/convoluin-Caffe:a-memo一个非常有趣的阅读来自于Yanqing Jia本人(Caffe的创始人)关于这个决定的起源,以及关于“临时”解决方案的想法。
加速GEMM
原始的方法
在这篇文章的其余部分,我将假设GEMM被执行为
和之前一样,首先让我们对基本的,课本上的矩阵乘法进行计时:
for i in 0..M:
for j in 0..N:
for k in 0..K:
C[i, j] += A[i, k] * B[k, j]使用Halide:
Halide::Buffer C, A, B; Halide::Var x, y; C(x,y) += A(k, x) *= B(y, k); // loop bounds, dims, etc. are taken care of automatically
最里面的一行执行2个浮点运算(乘法和加法),并执行M∗N∗K次,因此这个GEMM的FLOPs是2MNK。
我们来测量一下它在不同矩阵大小下的性能:
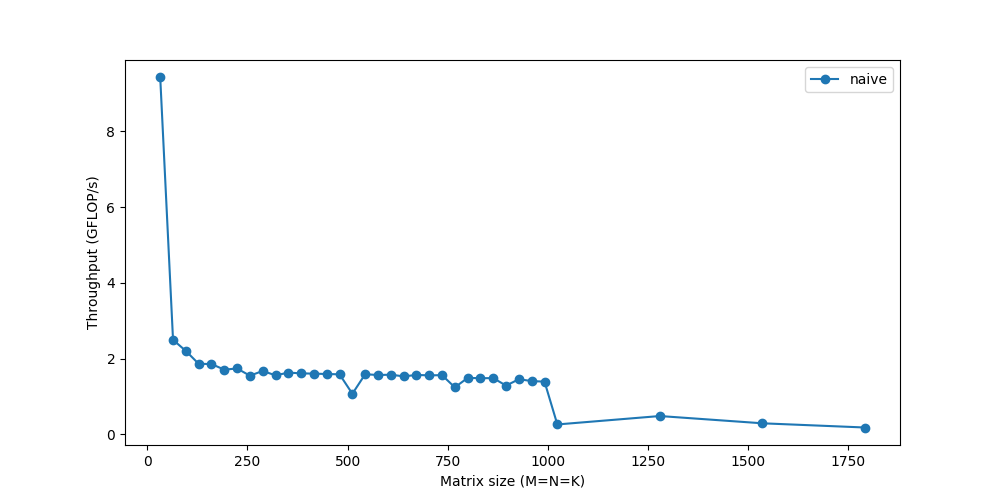
我们的性能才刚刚达到顶峰的10% !虽然我们将研究使计算更快的方法,但一个反复出现的主题是,如果我们不能快速获得数据,仅仅快速计算数据是不够的。由于内存对于较大的矩阵来说是一个越来越大的问题,因此性能会逐渐下降。你最后看到的急剧下降,表示当矩阵变得太大而无法放入缓存时,吞吐量突然下降—你可以看到系统阻塞。
缓存
RAM是一个大而慢的存储器。CPU缓存的速度要快几个数量级,但要小得多,因此正确使用它们至关重要。但是没有明确的指令说“加载数据以缓存”。它是一个由CPU自动管理的进程。
每次从主存中获取数据时,CPU都会自动将数据及其相邻的内存加载到缓存中,希望利用引用的局部性。
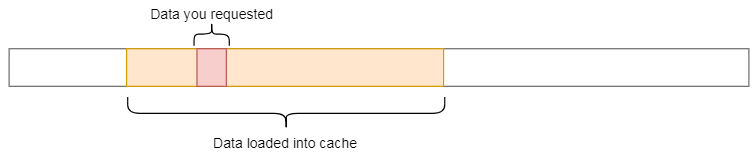
你应该注意的第一件事是我们访问数据的模式。我们在A上按行遍历,在B上按列遍历。
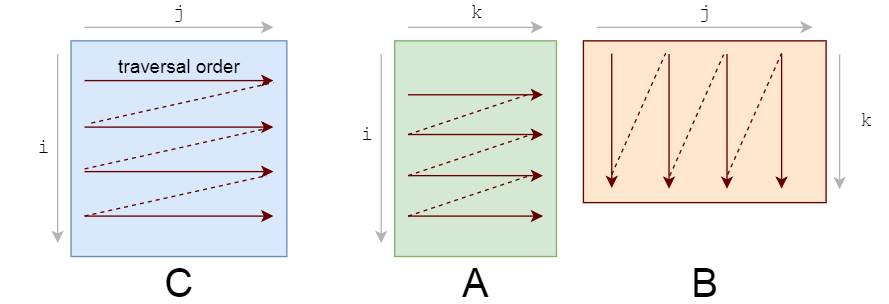
它们的存储也是行主序的,所以一旦找到A[i, k],行中的下一个元素A[i, k+1]就已经缓存了。酷。但看看B会发生什么:
- 该列的下一个元素没有出现在缓存中—在获取数据的时候,我们得到一个cache miss和CPU stalls。
- 一旦数据被获取,缓存也被填充在同一行B的其他元素。我们实际上不会使用它们,所以它们很快就会被驱逐。经过几次迭代之后,当实际需要它们时,我们将再次获取它们。我们正在用不需要的值污染缓存。
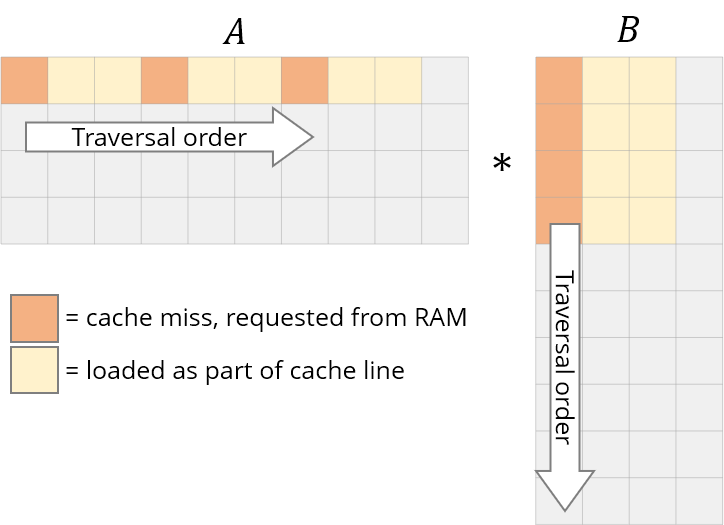
我们需要重新设计循环来利用这种缓存能力。如果正在读取数据,我们不妨利用它。这是我们要做的第一个更改:循环重新排序。
让我们重新排序循环,从i,j,k到i,k,j:
for i in 0..M:
for k in 0..K:
for j in 0..N:我们的答案仍然是正确的,因为乘法/加法的顺序无关紧要。遍历顺序现在看起来是这样的:
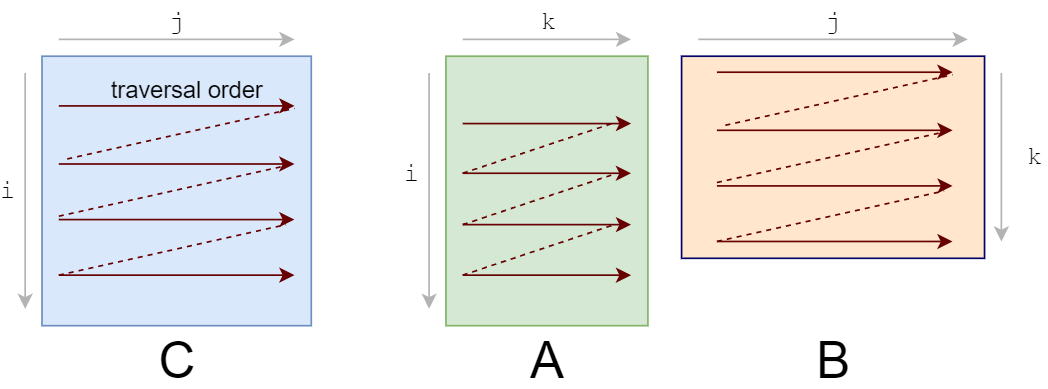
这个简单的改变,只是重新排序了一下循环,给了一个相当快的加速:
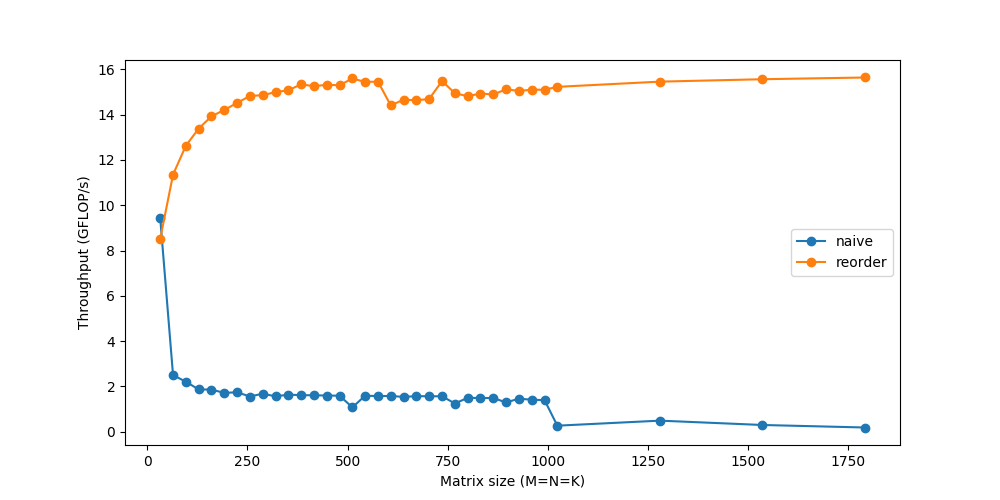
Tiling
为了进一步改进重新排序,我们还需要考虑一个缓存问题。
对于A的每一行,我们循环遍历整个B。在B中每进行一步,我们将加载它的一些新列并从缓存中删除一些旧列。当我们到达A的下一行时,我们从第一列开始重新开始。我们重复地从缓存中添加和删除相同的数据,这叫做抖动。
如果我们所有的数据都能放入缓存,就不会发生抖动。如果我们使用更小的矩阵,他们就可以幸福地生活在一起,而不会被反复驱逐。谢天谢地,我们可以分解子矩阵上的矩阵乘法。计算一个C中的小的r×c块,只需要A中的r行和B中的C列。让我们把C分成6x16的小块。
C(x, y) += A(k, y) * B(x, k);
C.update()
.tile(x, y, xo, yo, xi, yi, 6, 16)
/*
in pseudocode:
for xo in 0..N/16:
for yo in 0..M/6:
for yi in 6:
for xi in 0..16:
for k in 0..K:
C(...) = ...
*/我们已经把x,y的维度分解成外部的xo,yo和内部的xi,yi。我们将努力为较小的6x16块(标记为xi,yi)优化一个微内核,并在所有块上运行该微内核(由xo,yo迭代)。
Vectorization & FMA
大多数现代cpu都支持SIMD,或者Single Instruction Multiple Data。顾名思义,SIMD可以在相同的CPU周期内对多个值同时执行相同的操作/指令(如add、multiply等)。如果我们可以一次运行4个数据点上的SIMD指令,那么就可以实现4倍的加速。
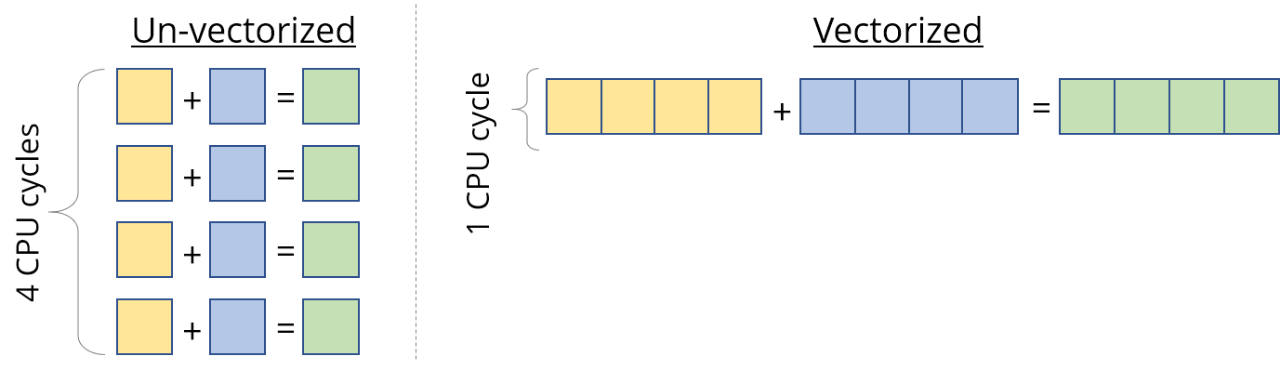
因此,当我们计算处理器的峰值速度时,我们“有点”作弊,而是参考了这种向量化的性能。这对于像向量这样的数据非常有用,我们必须对每个向量元素应用相同的指令。但是我们仍然需要设计内核来正确地利用这一点。
我们在计算峰值故障时使用的第二个“hack”是FMA-Fused Multiply-Add。虽然乘法和加法被算作两个独立的浮点运算,但它们是如此常见,以至于可以使用专用的硬件单元来“融合”它们,并将它们作为一条指令执行。使用它通常由编译器处理。
在Intel cpu上,我们可以使用SIMD(称为AVX & SSE)在一条指令中处理多达8个浮点数。编译器优化通常能够自己识别向量化的机会,但为了确保这一点,我们将亲自动手。
C.update()
.tile(x, y, xo, yo, xi, yi, 6, 16)
.reorder(xi, yi, k, xo, yo)
.vectorize(xi, 8)
/*
in pseudocode:
for xo in 0..N/16:
for yo in 0..M/6:
for k in 0..K:
for yi in 6:
for vectorized xi in 0..16:
C(...) = ...
*/
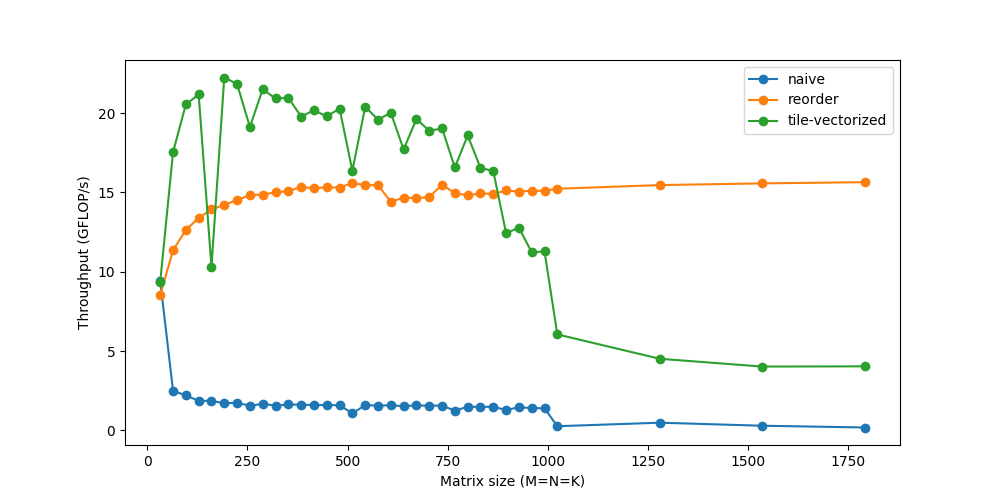
Threading
到目前为止,我们只使用了一个CPU内核。我们有多个可用的内核,每个内核可以同时物理地执行多个指令。一个程序可以把自己分成多个线程,每个线程可以运行在一个单独的内核上。
C.update()
.tile(x, y, xo, yo, xi, yi, 6, 16)
.reorder(xi, yi, k, xo, yo)
.vectorize(xi, 8)
.parallel(yo)
/*
in pseudocode:
for xo in 0..N/16 in steps of 16:
for parallel yo in steps of 6:
for k in 0..K:
for yi in 6:
for vectorized xi in 0..16 in steps of 8:
C(...) = ...
*/你可能会注意到,对于非常小的大小,性能实际上会下降,因为在较小的工作负载下,线程的工作时间更少,而彼此同步的时间更多。在线程方面还有很多其他类似的问题,它们本身可能需要进一步深入研究。
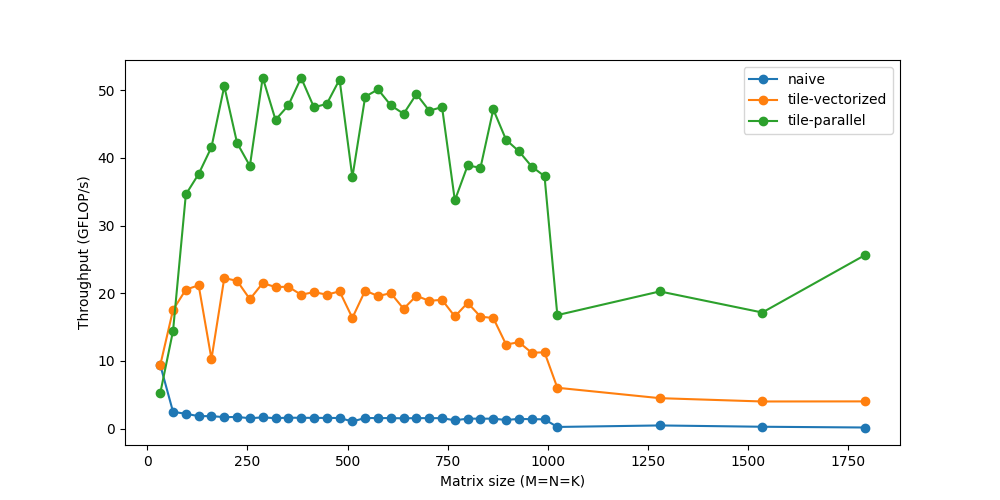
Unrolling
循环让我们避免了一遍又一遍地编写同一行的痛苦,同时引入了一些额外的工作,比如检查循环终止、更新循环计数器、指针算法等。相反,如果我们手工编写重复循环语句并展开循环,我们可以减少这种开销。例如,我们可以运行包含4个语句的2个迭代,而不是1个语句的8个迭代。
起初,我感到惊讶的是,如此反复无常、看似微不足道的管理费用,实际上却很重要。然而,尽管这些循环操作可能“便宜”,但它们肯定不是免费的。如果你还记得这里迭代的数量是以百万为单位的,那么每次迭代额外的2-3条指令的成本将很快增加。当循环开销变得相对较小时,好处会逐渐减少。
展开是另一个优化,现在几乎完全由编译器来处理,除了在像我们这样的微内核中,我们更喜欢控制。
C.update()
.tile(x, y, xo, yo, xi, yi, 6, 16)
.reorder(xi, yi, k, xo, yo)
.vectorize(xi, 8)
.unroll(xi)
.unroll(yi)
/*
in pseudocode:
for xo in 0..N/16:
for parallel yo:
for k in 0..K:
C(xi:xi+8, yi+0)
C(xi:xi+8, yi+1)
...
C(xi:xi+8, yi+5)
C(xi+8:xi+16, yi+0)
C(xi+8:xi+16, yi+1)
...
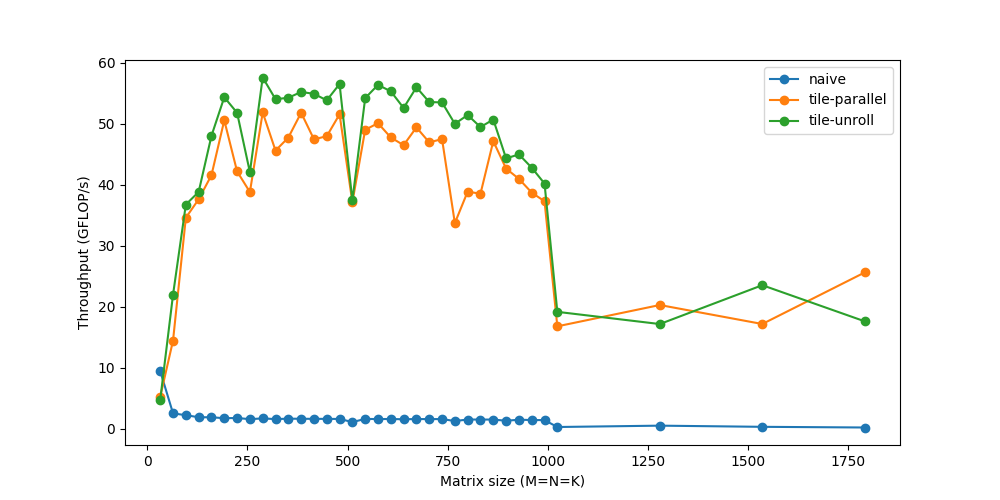
C(xi+8:xi+16, yi+5)
*/我们现在可以达到60GFLOP/s。
全部放到一起
上面的步骤涵盖了一些最常用的转换来提高性能。它们通常以不同的方式组合在一起,从而产生越来越复杂的策略来计算相同的任务。
这是来自Halide 的一个更仔细优化的策略。
matrix_mul(x, y) += A(k, y) * B(x, k);
out(x, y) = matrix_mul(x, y);
out.tile(x, y, xi, yi, 24, 32)
.fuse(x, y, xy).parallel(xy)
.split(yi, yi, yii, 4)
.vectorize(xi, 8)
.unroll(xi)
.unroll(yii);
matrix_mul.compute_at(out, yi)
.vectorize(x, 8).unroll(y);
matrix_mul.update(0)
.reorder(x, y, k)
.vectorize(x, 8)
.unroll(x)
.unroll(y)
.unroll(k, 2);总结一下,它是这样做的:
- 分裂成32x24的小块。进一步将每个tile分成8x24个子tile
- 在临时缓冲区(matrix_mul)中计算8x24的matmul,使用类似的重新排序、向量化和展开
- 使用矢量化、展开等方法将临时的matrix_mul复制回out。
- 在所有32x24块上并行化这个过程
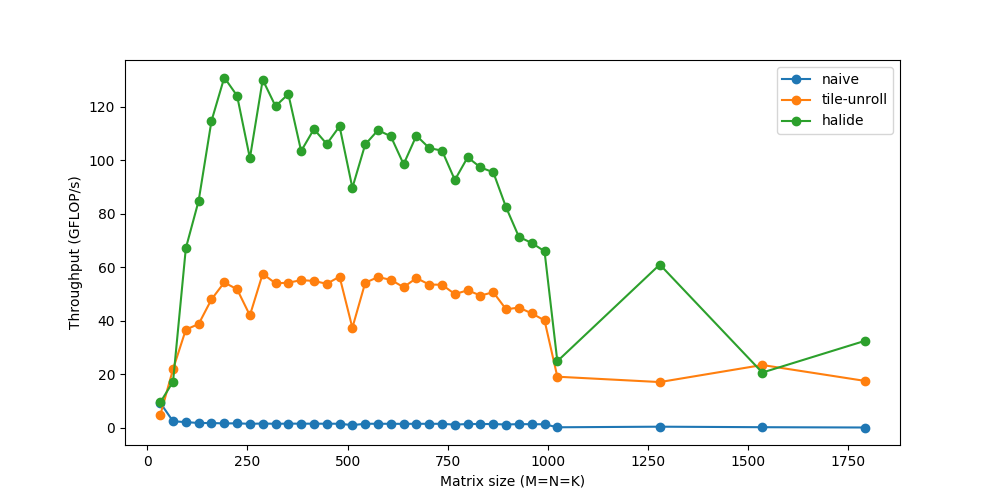
最后,我们能够达到超过120GFLOPs的速度—相当接近160 GFLOPs的峰值性能,并且能够匹配OpenBLAS等生产级库。使用类似的im2col微调代码,然后是gemm,相同的卷积现在运行时间为~20ms。如果你对这方面的研究感兴趣,可以尝试使用你自己的不同策略—作为一名工程师,我总是听到关于缓存、性能等方面的说法,看到它们的真实效果可能是有益的和有趣的。
注意,这种im2col+gemm方法是大多数深度学习库中流行的通用方法。然而,定制化是关键——对于特定的常用大小、不同的体系结构(GPU)和不同的操作参数(如膨胀、分组等),这些库可能会再次使用针对这些情况的类似技巧或假设进行更定制化的实现。这些微内核是经过反复试验和错误的高度迭代过程构建的。程序员通常只对什么应该/不应该工作得很好有一种直觉,并且/或者必须基于结果考虑解释。听起来很适合深度学习研究,对吧?
英文原文:https://sahnimanas.github.io/post/anatomy-of-a-high-performance-convolut...
本文转自:AI公园,原作者:Manas Sahni;编译: ronghuaiyang,转载此文目的在于传递更多信息,版权归原作者所有。






