不平衡样本的处理
机器学习中经典假设中往往假定训练样本各类别是同等数量即各类样本数目是均衡的，但是真实场景中遇到的实际问题却常常不符合这个假设。一般来说，不平衡样本会导致训练模型侧重样本数目较多的类别，而“轻视”样本数目较少类别，这样模型在测试数据上的泛化能力就会受到影响。一个例子，训练集中有99个正例样本，1个负例样本。在不考虑样本不平衡的很多情况下，学习算法会使分类器放弃负例预测，因为把所有样本都分为正便可获得高达99%的训练分类准确率。
下面将从“数据层面“和”算法层面“两个方面介绍不平衡样本问题。
数据层面处理办法
数据层面处理方法多借助数据采样法使整体训练集样本趋于平衡，即各类样本数基本一致。
数据重采样
简单的数据重采样包括上采样和下采样。由于样本较少类，可使用上采样，即复制该图像直至与样本最多类的样本数一致。当然也可以由数据扩充方式替代简单复制。对于样本较多的类别，可采用下采样，注意，对深度学习而言，下采样并不是直接随机丢弃一部分图像，因为那样做会降低训练数据多样性而影响模型泛化能力。正确的下采样方式为，在批处理训练时对每批随机抽取的图像严格控制其样本较多类别的图像数量。以二分为例，原数据的分布情况下每次批处理训练正负样本平均数量比例为5：1，如仅使用下采样，可在每批随机挑选啊训练样本时每5个正例只取1个放入该批训练集的正例，负例选取按照原来的规则，这样可使每批选取的数据中正负比例均等。此外，仅仅将数据上采样有可能会引起模型过拟合。更保险有效的方式是上采样和下采样结合使用。
类别均衡采样
把样本按类别分组，每个类别生成一个样本列表，训练过程中先随机选择1个或几个类别，然后从各个类别所对应的样本列表里选择随机样本。这样可以保证每个类别参与训练的机会比较均等。
上述方法需要对于样本类别较多任务首先定义与类别相等数量的列表，对于海量类别任务如ImageNet数据集等此举极其繁琐。海康威视研究院提出类别重组的平衡方法。
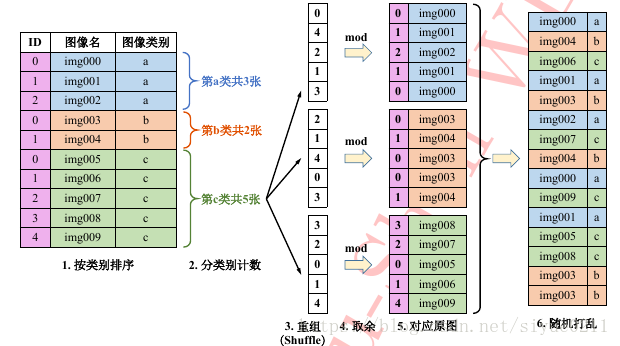
类别重组法只需要原始图像列表即可完成同样的均匀采样任务，步骤如下：
1. 首先按照类别顺序对原始样本进行排序，之后计算每个类别的样本数目，并记录样本最多那个类的样本数目。之后，根据这个最多样本数对每类样本产生一个随机排列的列表， 然后用此列表中的随机数对各自类别的样本数取余，得到对应的索引值。接着，根据索引从该类的图像中提取图像，生成该类的图像随机列表。之后将所有类的随机列表连在一起随机打乱次序，即可得到最终的图像列表，可以发现最终列表中每类样本数目均等。根据此列表训练模型，在训练时列表遍历完毕，则重头再做一遍上述操作即可进行第二轮训练，如此往复。 类别重组法的优点在于，只需要原始图像列表，且所有操作均在内存中在线完成，易于实现。
算法层面的处理方法
对于不平衡样本导致样本数目较少的类别”欠学习“这一现象，一个很自然的解决办法是增加小样本错分的惩罚代价，并将此代价直接体现在目标函数里。这就是代价敏感的方法，这样就可以通过优化目标函数调整模型在小样本上的注意力。算法层面处理不平衡样本问题的方法也多从代价敏感的角度出发。
代价敏感方法
代价敏感的方法可概括为两种， 一则基于代价敏感矩阵，一则基于代价敏感向量。
代价敏感矩阵
以分类问题为例，假设某训练集共有 N 个样本，形如
，其中样本标记 y 隶属于 K 类。基于代价敏感矩阵方法是利用 K ∗ K 的矩阵 C 对不同样本类别施加错分惩罚（亦可称权重）。
其中, C ( yi , yj ) ∈ [ 0,∞ ) 表示类别 yi 错分为类别 yj的惩罚。C ( yi , yi ) = 0 。施加代价后的训练目标变为：训练得到某分类器 g 使得期望之和 ∑n C ( yn, g ( xn) ) 最小。
代价敏感向量
另一种代价敏感的反映方式则针对样本级别:对某样本 ( xn , yn ) , 有对应的一个 K 维的代价敏感向量 cn ∈ [ 0 , +∞ )K , 其中 cn 的第 k 维表示该样本被错分为第 k 类的惩罚。基于代价敏感向量的方法在模型训练阶段是将样本级别的代价敏感向量与样本以 ( xn , yn , cn ) 三元组形式一同作为输入数据送入学习算法。细心的读者不难发现，代价敏感矩阵法实际上是代价敏感向量法的一种特殊形式,即对于某类的所有样本其错分惩罚向量为同一向量。
代价敏感法中权重的指定方式
代价敏感方法的处理前提是先指定代价敏感矩阵或向量。其中关键是错分惩罚或错分权重的设定。实际使用中可根据样本的比例，分类结果的混淆矩阵等信息指定代价敏感矩阵或向量中错分权重的具体取值。
按照比例指定
假设训练样本的标记共有3类：a类， b类， c类。它们的样本数目比例是3：2：1，则代价敏感矩阵为：
可以在矩阵基础上乘以类别最小公倍数6。
根据混淆矩阵指定
混淆矩阵(confusion matrix)是人工智能中一种算法分析工具， 用来度量模型或学习算法在监督学习中预测能力的优劣。 在机器学习领域，混淆矩阵通常也被称之为”联列表“ 或 ”误差矩阵“。混淆矩阵的每一列代表一个类的实例预测，而每一行代表其真实类别，如下表，仍以a， b， c三类分类为例。
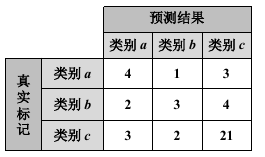
矩阵对角线为正确分类样本数，各分类为4， 3， 21。矩阵其它位置为错分样本数，如a错分b类的样本数为1， 错分c类的样本数为3。
虽然各类错分样本数的绝对数值接近（均错分3）但是相对而言，样本数较少的a类b类有50%和66.67%的样本被错分，比例相当高，但是c类只有19%。该情况用代价敏感法处理时，可根据各类分错样本数设置代价敏感矩阵的取值。
一种方法直接以错分样本数为矩阵取值。
不过更优的方案还需考虑各类的错分比例，并以此比例调整错分权重。对a类而言，a类错分比例50%，占所有比例的136%（50%+67%+19%）的百分之36.76%，
小结
数据层面采用数据重采样处理解决样本不平衡问题，其操作简单，不过该类方法会改变数据原始分布，有可能产生过拟合
算法层面采用代价敏感法处理样本不平衡问题，通过指定代价敏感矩阵或代价敏感向量的错分权重，可缓解样本不平衡带来的影响。
参考文献
解析卷积神经网络——深度学习实践手册
版权声明：本文为CSDN博主「四月晴」的原创文章，遵循CC 4.0 by-sa版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/siyue0211/article/details/80318999
