梯度下降方法是机器学习中常用的参数求解方法。本文将从四个方面为大家详细介绍梯度下降的算法理论,具体包括:
① 梯度下降方法原理
② 关于梯度,为什么负梯度方向是下降最大方向?
③ 实践,以回归分析为例
④ 梯度下降的其他问题
1、梯度下降方法原理
在机器学习算法中,我们在定义损失函数后,需要对损失函数最小化进行参数求解。而梯度下降法是在无约束优化问题时的经典方法。

只要上述过程不断执行下去总能收敛到局部极小值(为什么是局部极小值而不是全局最小值?下面再探讨)因此现在的问题就转化为沿着哪个方向更新 x,能够使得函数值f(x)下降得最快?
答案是负梯度下降方向。

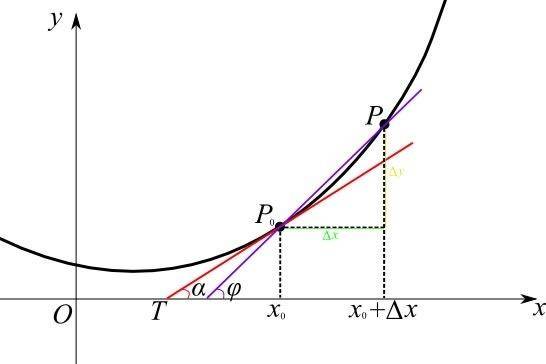
梯度下降过程示意图:

如上图,事实上梯度下降过程就好像从山上某一起点要下到山下的最低点。当然,从起到到最低点存在很多条路,那么我们应该怎么走呢?一个方法就是开始时,环顾四周,先找到一个下降最快的方向,之后沿着这个方向走一步。走一步后,再重新环顾四周,再找到一个下降最快的方向,于是再走一步。之后不断重复这个过程,直到你发现去到某一个点,环顾四周,方向都比你高,则认为到达终点了。
具体来说,梯度下降算法步骤如下:

从上式中可以发现迭代的三个停止条件:
(1) 梯度小于指定阈值;
(2) 目标函数变化小于指定阈值;
(3) 迭代变量x小于指定阈值;
值得注意的是,当目标函数是凸函数时,梯度下降法的解释全局最优解,这是没有问题的。但是在很多情况下,我们通过梯度下降到达的不一定是全局最低点,而是局部最低点,如下图所示,分别从A点和B点出发,通过若干次后迭代后,分别落于全局最低点和局部最低点。

2、为什么负梯度方向是下降最大方向?
要完整理解梯度,我们将从导数开始针对梯度进行推导:
• 导数及偏导数
• 方向导数
• 梯度
1. 导数及偏导数
在正式讲解梯度之前,我们先对导数进行讨论:
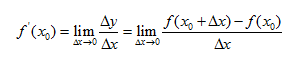

不过由于是一元函数,因此也就只有一个方向变动。接下来,我们讨论二元函数上不同方向的变化,接下来,我们进入到二元函数领域,进一步介绍偏导数:

同样把偏导数转为为图像有:


实际上,我们已经发现了偏导数是多元函数沿着坐标轴方向上的变化率,但在实际情况中,我们不仅要知道多元函数在坐标轴上的变化率,还希望知道在其他特定方向上的变化率,这就引出了下一个概念,方向导数。
2. 方向导数


证明:

3. 梯度
接下来,回答最后一个问题,在多元函数的曲平面上,哪个方向是函数变化最快的方向?

因此我们把向量f定义为函数 g 的梯度。因此我们说梯度方向是函数增长最快的方向,而负梯度方向则是函数降低最快的方向。
3、实例,以回归分析为例
对于多元回归分析,我们有回归公式如下所示:

针对于该方程中的未知参数,我们可以利用最小二乘法进行估计,损失函数方程有:
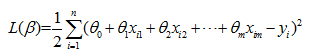
有梯度下降公式如下:
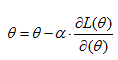
对于第 j 个变量,有:

所以有更新公式如下:
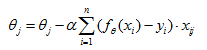
在实际应用当中,梯度下降有三种方式分别是批量梯度下降(BatchGradient Descent,BGD),随机梯度下降(StochasticGradient Descent,SGD)以及小批量梯度下降(Mini-batchGradient Descent,MBGD)
1)批量梯度下降:最经典的梯度下降方法,就是就上述例子所使用的计算公式,在计算时,每次更新都使用所有的样本进行计算,仍以回归分析为例,有:
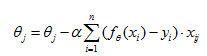
2)随机梯度下降:是批量梯度下降的一个变体,相对于批量梯度下降需要使用所有的样本进行更新,随机梯度下降每次更新只使用一个样本进行计算:
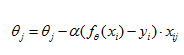
相比于批量梯度下降,由于随机梯度下降每次只使用一个样本进行迭代更新,因此训练速度要比批量梯度下降快得多,但是也由于每次只使用一个样本更新,需要的迭代次数将增加(但整体迭代时间还是要比批量梯度下降更快),同而且得到的解可能并非最优解。
3)小批量梯度下降:批量梯度下降和随机梯度下降实际上就是两个极端,一个使用所有样本,另一只使用一个样本,而小批量梯度下降则可以视为两种方法的折中,我们将使用 k 个样本进行更新:
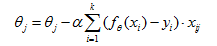
4、梯度下降的其他问题
1)初始点的选择:初始点的选择没有确定的方法。当初始点距离最优点较近的时候,可以获得更快的收敛速度。对于凸问题,任意初始点都能获得最优解,而对于非凸问题,则只有在最优点的邻域内才能获得最优解,否则只是局部最小。在实验中,可以尝试选择多个不同值作为初始点进行训练,选择能够获得损失函数最小值的初始点作为初始点。
2) 学习率的选择:学习率既可以选择固定值,也可以选择自适应方法。一般来说,自适应方法的迭代的早期会设定较大的步长,而随着迭代次数的增加,则慢慢减小步长,防止错过最优解。
本文转自:探数寻理(微信号:wetalkdata),作者:浩彬老撕,转载此文目的在于传递更多信息,版权归原作者所有。






