来源:towardsdatascience
编译:Simons’Road
如今,即便是结构非常复杂的神经网络,只要使用Keras,TensorFlow,MxNet或PyTorch等先进的专业库和框架,仅需几行代码就能轻松实现。而且,你不需要担心权重矩阵的参数大小,也不需要刻意记住要用到的激活函数公式,这可以极大的避免我们走弯路并大大简化了建立神经网络的工作。然而,我们还是需要对神经网络内部有足够的了解,这对诸如网络结构选择、超参数调整或优化等任务会有很大帮助。本文我们将会从数学角度来充分了解神经网络是如何工作的。
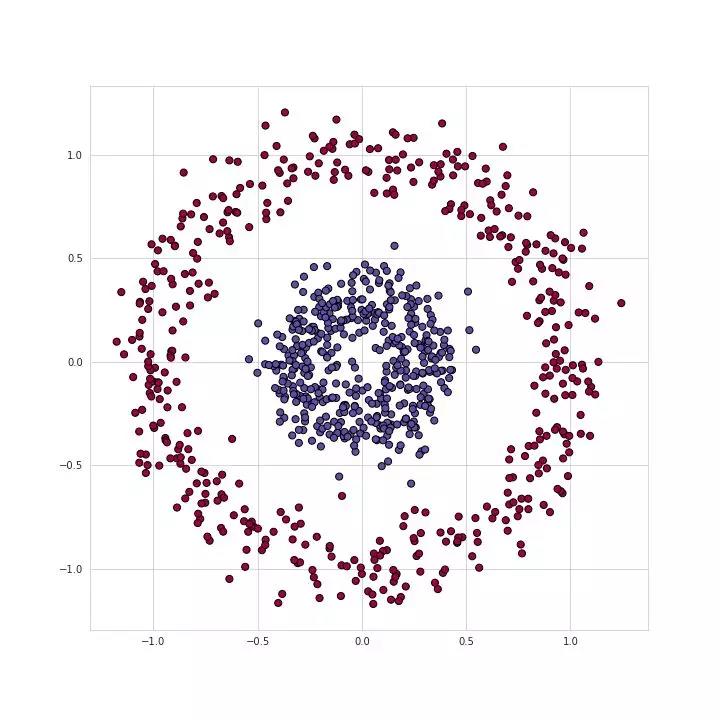
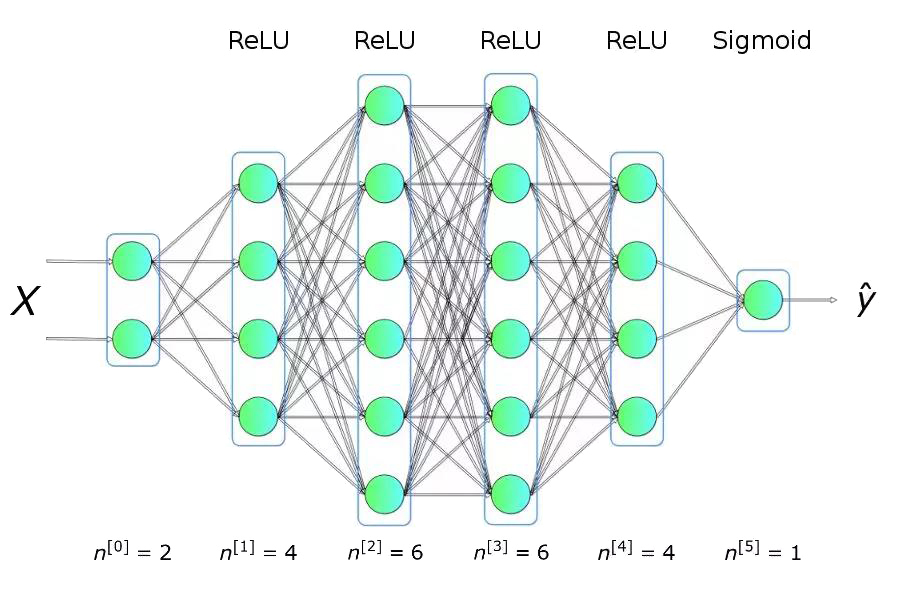
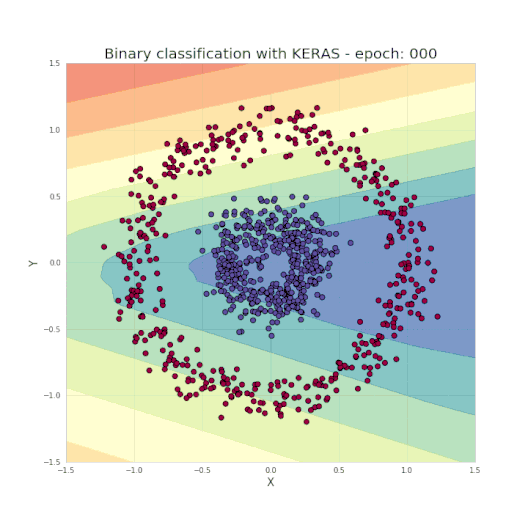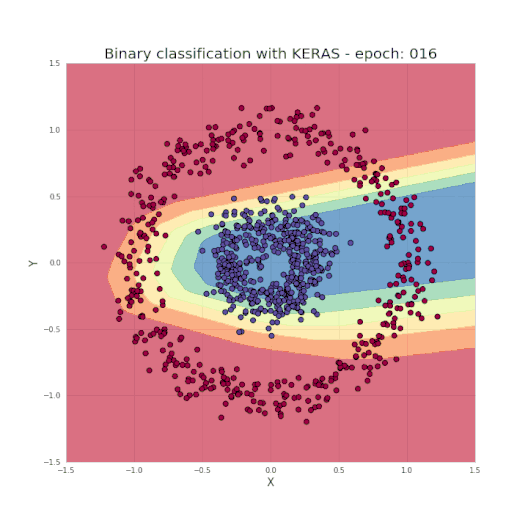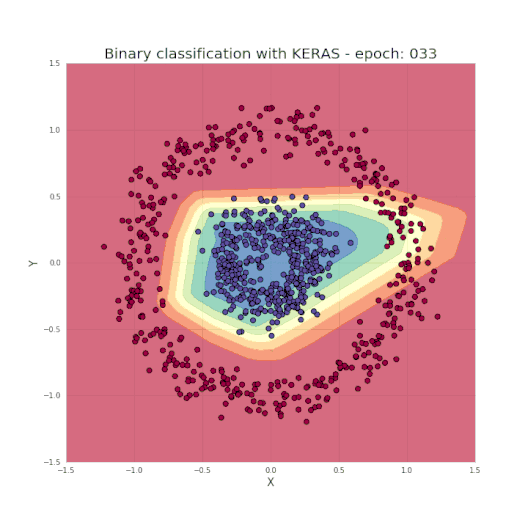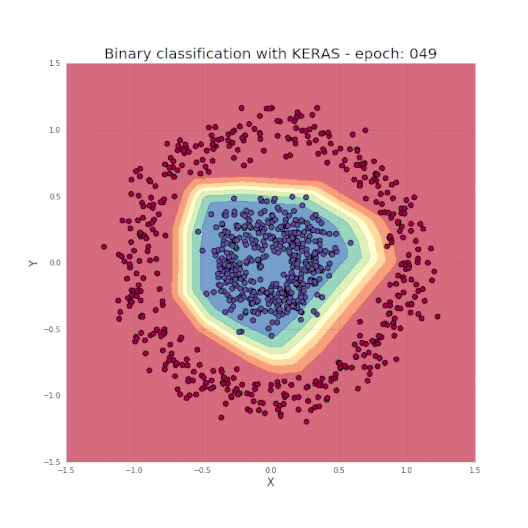
如图1所示,是一个典型的数据二分类问题,两类的点分别形成了各自的圆,这种数据分布对于许多传统的机器学习算法来说很难,但对于轻量级的神经网络却很容易胜任。为了解决该问题,我们将使用具有图2所示结构的神经网络,包括五个全连接层,每层具有不同数量的单元。对于隐藏层,我们将使用ReLU作为其激活函数,而使用Sigmoid作为输出层。 这是一个非常简单的结构,但对于我们要解决的问题而言却已经拥有足够的能力了。
正如之前提到的,只需几行代码便足以创建和训练一个模型,就能实现测试集中的分类结果几乎达到100%的准确度。而我们的任务,就是为所选的网络设定超参数,如层数、每层的神经元数、激活函数和迭代次数等。现在让我们看一个很酷的可视化,来看看学习过程究竟发生了什么。
什么是神经网络?
让我们首先回答这个关键问题:什么是神经网络? 它是一种在生物学启发下构建计算机程序的方法,能够学习并找到数据中的联系。 如图2所示,网络是按层排列的“神经元”的集合,通过权重互联互通的联系在了一起形成网络。
每个神经元接收一组编号从1到n 的x值作为输入,用来计算预测的y^值。向量x实际上包含来自训练集的m个样本之一的特征值。比较重要的是,每个神经元都有自己的一组参数,通常称为w(权重列向量)和b(偏差),它们会学习过程中发生变化。每次迭代中,神经元基于其当前权重向量w来计算输入向量x加权平均后的值并加上偏置b。最后,该计算结果会通过非线性激活函数g,本文的后面部分会提及一些最常用的激活函数。
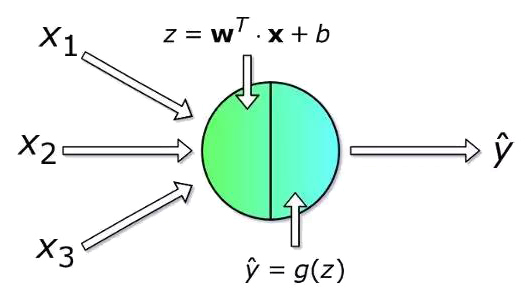
我们已经对单个神经元的工作有所了解了,下面让我们再深入学习一下如何对整个神经网络层进行计算,并将所有图进行向量化,最后将计算合并到矩阵方程中。 为了统一符号,方程中[l]表示为所选层,下标表示该层中神经元的索引。
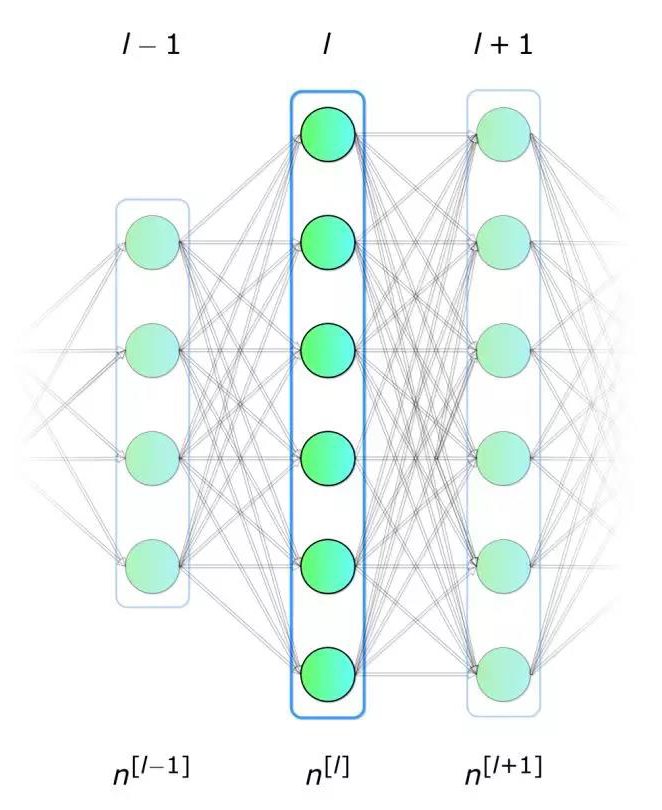
对单个单元而言,我们使用x和y^分别表示特征列向量和预测值。然后使用向量a表示相应的层,而向量x对应层0的输入,即输入层。层中的每个神经元根据以下等式执行计算:
为了清楚起见,以第2层为例展开:

如您所见,对于每层我们都必须执行类似操作,那么使用for循环效率就会不高。为了加快计算速度,我们将使用向量化的方法。 首先,通过将转置后的权重w行向量堆叠在一起就 构建得到矩阵W. 类似地,我们将层中的每个神经元的偏置堆叠在一起,从而得到列向量b。 这样我们就能构建出一个矩阵方程,能够一次便对层中所有神经元进行计算。下面我们写下使用的矩阵和向量的维数。

到目前为止,得到的方程只适用于这一个例子。 在神经网络的学习过程中,您通常使用大量数据,最多可达数百万条。因此,下一步要做的将是跨多个示例的矢量化。 假设我们的数据集包含m个示例,每个示例都具有nx特征。首先,我们将每层的列向量x,a和z组合在一起,分别创建X,A和Z矩阵,然后我们重写先前的方程。

激活函数
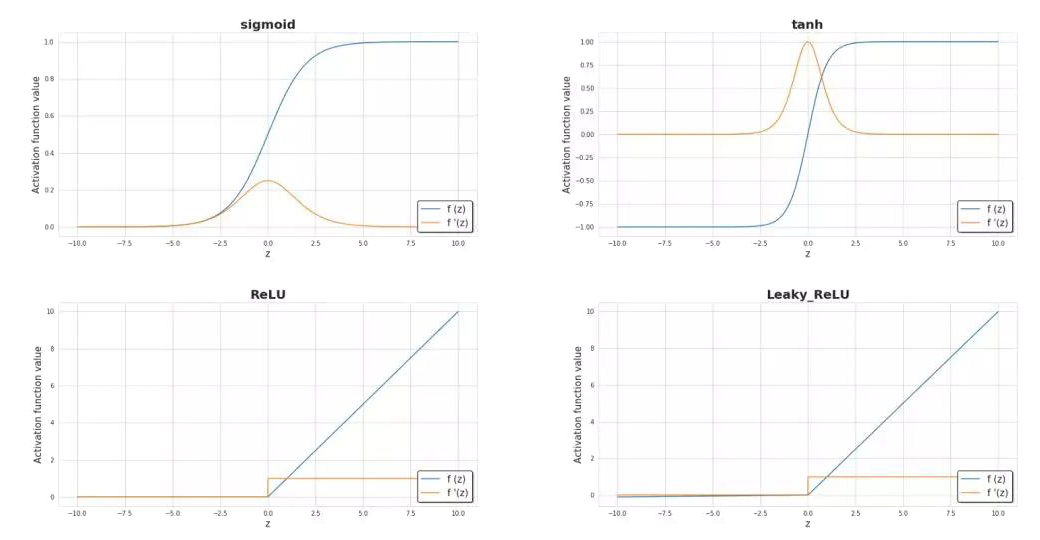
激活函数是神经网络的关键元素之一。没有它们,我们的神经网络只能成为线性函数的组合,就只能具备有限的扩展性,也不会拥有超越逻辑回归的强大能力。引入非线性元素则会使得学习过程中拥有更大的灵活性和创建复杂表示的功能。 激活函数也会对学习速度产生重大影响,这也是主要的选择标准之一。下图6中,显示了一些常用的激活函数。目前,最受欢迎的隐藏层可能是ReLU。但如果我们要处理二分类问题时,尤其是我们希望从模型返回的值在0到1的范围内时,我们有时仍然使用sigmoid激活函数。
损失函数
我们主要通过损失函数的值来观察学习过程的进展。一般来说,损失函数旨在显示我们与“理想”解决方案的距离。在本文的例子中,我们使用二进制交叉熵作为损失函数,但根据不同的问题可以应用不同的函数。本文使用的函数由下列公式描述,并且在学习过程中其值的变化过程可视化显示在图7中,显示了损失函数如何随迭代次数而准确度逐渐提高。
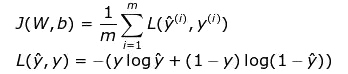
神经网络是如何学习的?
整个学习过程是围绕如何调整参数W和b使得损失函数最小化进行的。为了实现这一目标,我们将结合微积分并使用梯度下降法来找到函数最小值。在每次迭代中,相对于神经网络的每个参数计算损失函数对应的偏导数值。导数具备很好的描述函数斜率的能力。通过可视化,我们可以清楚地看到梯度下降是如何改变参数变量使得目标函数的值在图中向下移动。如图8所示,可以看到每次成功的迭代都朝着最小值点方向进行。在我们的神经网络中,它以相同的方式工作,每次迭代时计算的梯度代表应该移动的方向。主要区别在于,在我们的神经网络范例中,我们有更多的参数需要操作。因此变得更为复杂,那么究竟怎样才能计算出最优参数呢?
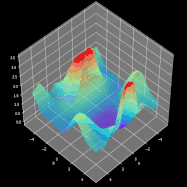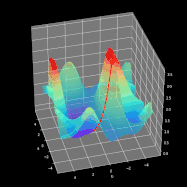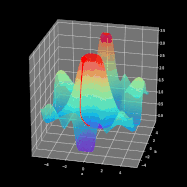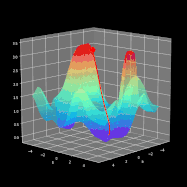
这时候我们就需要引入计算最优参数的算法——反向传播(BP),它允许我们计算一个非常复杂的梯度,也正是我们需要的。根据以下公式来调整神经网络的参数。

在上面的等式中,α表示学习率,这个超参数可以自定义调整。选择合适的学习率是至关重要的,如果我们将其设置得太低,那么我们的神经网络会学习得非常慢,如果设置得太高那么损失函数就不会到达最小值了。 dW和db分别是W和b相对于损失函数的偏导数,可以上述公式推导而的。 dW和db的尺寸也是分别和W和b对应的。图9显示了神经网络中的操作顺序,我们可以清楚地看到前向传播和反向传播是如何协同工作以优化损失函数的。
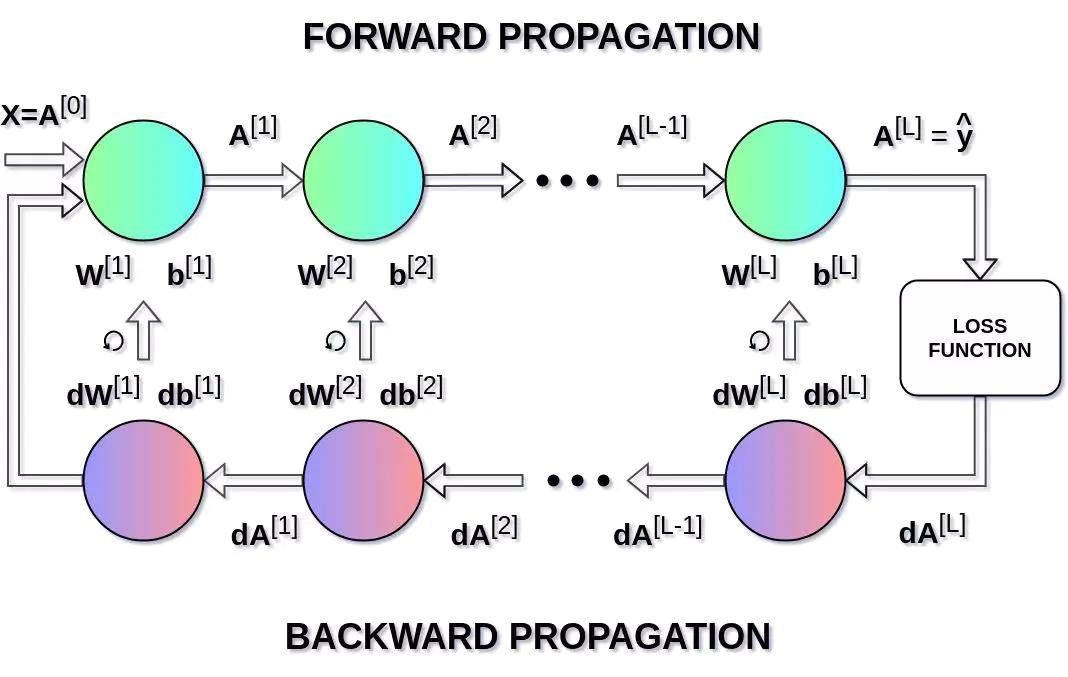
通过前向传播的预测和反向传播纠正信号,就能不断的根据数据来调整网络,最终实现了神经网络从数据中学习的能力。
在使用神经网络时,至少要了解内部运行过程的基础知识才能得心应手。尽管在本文中提到了一些比较重要的知识,但这仅仅是冰山一角。 如果希望深入理解神经网络的运行机理,请使用像Numpy一样的基础工具来编写一个自己的小型神经网络吧!你会得到想不到的收获!
本文转自: 将门创投,转载此文目的在于传递更多信息,版权归原作者所有。