作者:PengChao
2019年的时针开始转动,在CNN、RNN、LSTM、GAN、GNN、CAP的潮起潮落中,带来了这篇博客。放上一篇 参考引用 。 其实个人认为理解GNN的核心问题就是理解图怎么做傅里叶变换。CNN的核心操作时卷积,GNN也是。CNN计算二维矩阵的卷积,GNN计算图的卷积。那么我们定义好图的傅里叶变换和图的卷积就可以了,其媒介就是图的拉普拉斯矩阵。
好了,这篇博客将简要介绍图神经网络的原理,但是不会设计太多数学细节(因为博主数学很烂啦)。通过理解图神经网络的卷积操作,来理解其流程,再会配合代码来做简单解释。
拉普拉斯矩阵
对于一个图来说,其度为其与顶点链接的数量,Degree Matrix的对角线元素就是其每个顶点度的数量。邻接矩阵表示了图中各个顶点的邻接关系。如下图,一个图的Laplace矩阵就是 L = D – A。

事实上,常用的Laplace矩阵有三种,上面介绍的只是其中一种。
Laplace矩阵有许多良好的性质:
1. Laplace矩阵是对称矩阵,可以进行特征分解
2. Laplace矩阵只在中心顶点和一阶相连顶点上有非0元素,其余处均为0
3. Laplace算子与Laplace矩阵进行类比
图的傅里叶变换
推广傅里叶变换
传统的傅里叶变换针对连续的函数,然后对数列有了离散傅里叶变换,那么矩阵能否做傅里叶变换呢?这篇Paper告诉我们,可以,没问题:https://arxiv.org/abs/1211.0053
L时拉普拉斯矩阵,V是其特征向量,满足 LV=\lambda V
L的拉普拉斯谱分解为 L = U \sigma U^T
那么定义Graph上的傅里叶变换为Fourier(f) = U^T f
推广卷积(f*h)_G = U((U^Th)\odot(U^Tf))
那么时域上的卷积就是频域点乘的傅里叶逆变换,这样我们就可以实现卷积操作了。
理解拉普拉斯矩阵谱分解
傅里叶变换的本质,就是把任意一个函数表示成若干正交函数(由sin,cos构成)的线性组合。
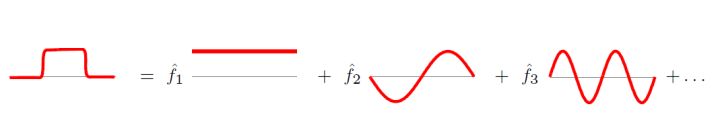
拉普拉斯矩阵的特征值表示频率。再graph空间上无法可视化频率的概念,信息论告诉我们,特征值越大,对应的信息越多,小的特征值就是低频分量,信息较少,是可以忽略的。
在压缩图像的过程中,也是把低频成分变为0,高频(边缘)会被保留,它带给我们更多的信息。
Deep Learning 中的 Graph Convolution
在卷积和中,需要手工设置K个参数,K具有很好的spatial localization,对应的有权重系数(这些具体的参数根据模型会有不同,这里大致介绍,重在理解)。更直观的看,K=1就是对每个顶点上一阶neighbor的feature进行加权求和,如下图


GCN每次卷积对所有顶点都完成了图示操作。
进一步在数学层面上理解Spectral Graph在GCN中的作用,这个就参考开头给出链接中的paper吧。
OK,See You Next Time!
本文转自:DEEP STUDIO,作者:PengChao,转载此文目的在于传递更多信息,版权归原作者所有。






