要知识点:
- 辐射量的定义
- 双向反射分布函数
- 理想的漫反射BRDF实现
- 理解什么是渲染方程
- 如何解渲染方程
- 初步了解蒙特卡洛积分
辐照理论概念基础
在讲解相关理论模型前,首先介绍下我理解的颜色。首先真实世界是不存在颜色的,人眼感知到的不同颜色只不过是电磁波的不同频率(f)而已,由此可以得出一个重要结论就是颜色只不过是人的主观感受,并不是事物的客观属性,物体只是在发射或者反射电磁波。下图(1)展示的是目前人类能够感知的颜色对应的电磁波频率,也称为可见光频段。

既然颜色只不过是不同频率的电磁波而已,那么人眼又是怎么将可见的颜色与可见光上的频率对应起来呢?首先色彩有三要素:色相(实质即电磁波频率)、亮度(顾名思义颜色的亮度电磁波的振幅,幅度越大就越亮也可以理解为同一时刻人眼接收同一个频率的电磁波数量,可以想象成波的叠加导致波的振幅增大)、饱和度(颜色中白光的比例,饱和度低,白光占比越多,颜色就发白)[1]。
了解了颜色的本质后,那么为了在计算机显示器上渲染出接近现实世界的场景图片,就得通过适当的模型来进行计算,辐射度理论模型就是其中一种,该模型是以能量守恒物理定律为基础建立的,观察前辈们提出的各种理论模型可发现,要想模拟现实世界,只能是以现实世界客观规律为出发点,才会得到想要模拟的目标。该模型也是射线追踪渲染算法重要理论基础,也是接下来本文重点讨论的重点。说到理论基础当然避免不了使用微分和积分(单重积分、多重积分),因为微积分是进行辐射度理论推导和讨论的最为严谨的数学工具。
在介绍辐射度模型之前首先需要介绍一些基本物理概念:
① 辐射能量(Q):是电磁波能量的单位用符号(J 焦耳)表示。 每个光子携带的辐射能量为 Q = hc/λ ( h = 6.62620x10-34 是普朗克常量, c 表示光速2.98x108m/s , λ 表示波长,频率 f = c / λ )所以 Q 也可以表示为 hf。根据前面说的颜色本质(人眼对不同可见频段的电磁感知),按照这个公式 Q = hf 可知,颜色就是人眼接收到含有相应能量的辐射。
② 辐射通量(Φ):(我喜欢称为辐射功率,后面我会统一称为辐射功率):辐射能量Q每秒通过表面s的量,用Φ = dQ / dt表示,单位是(W 瓦特)。由于辐射通量也可以用于度量光源每秒发射的能量,所以也就称为辐射功率。电磁波的频率是光量子每秒钟振动次数,所以有定义可知单个光量子辐射功率是一个常量。
③ 辐射功率密度(M):单位表面积A上的辐射功率(单位W*m-2),数学表示是M = dΦ / dA , dA 表示微分面积。由数学定义可知,这个公式并不局限于真实空间的表面,也可以是想象的空间表面,也被称为发光度B。有这个定义可知,这个量是用来表示亮度的,定义用通俗的话说就是人眼颜色感知细胞同时接收到的光线数量。
④ 辐照功率密度(E):空间表面接收的辐射功率密度 E = dΦ/dA,单位和定义3一样
⑤ 辐射密度(I):单位立体角的辐射功率I=dΦ/dω,单位是 W*sr-1。(注:立体角Solid Angle可以看成是二维弧度到三维的扩展,所以可以将其理解成三维弧度上图中的一小块面积等于:dA2= rdθ *rsinθdφ,从图中可以看出 dA2 是球面上微小面积,所以整个球面对微小面积进行积分 A = ∫dA2 = 4PI(就是球面积 S = 4PIr2 它是一个和球半径无关的量,也可以理解成球面上的一块区域边界到球心的连线形成的类椎体的尖锐程度)。当球心放置的发光体功率 Φ 一定时,那么其对整个球体的辐射密度也是一定的 I = Φ/4PI。也就是说从任一一个方向看这个球心的发光体,不管从多远看,眼睛就收到的光的频率都是一样,这也说明了这个物理量是用于表示颜色的

⑥ 辐射率(L): 定义单位面积内的辐射密度I,单位是(W*m-2*sr-1)。前面定义了辐射功率密度E表示亮度,然后又定义了辐射密度I表示色相,根据前面颜色介绍可知,颜色三个要素是色相、亮度、饱和度(可以忽略)。那么完整的颜色表示的物理量就是 L = d2Φ/(dAτ*dω) 。在射线追踪算法中则使用RGB值来表示辐射率的。(RBG可以 用来表示色相、和亮度)

辐射率与角度
当p是曲面上一点时,如果使用曲面的上的面微分dA代替
中的dAτ 将是非常方便的。考虑辐照功率密度E照射在曲面S的微小面片上se,se的法线为n.当E是垂直于se时,dAτ 和dA相等 。如下图(a)所示,当E照射方向与 se 法线成 θ 角时,
这个定律也被称为Lambert定律。由此可得任意表面辐射率公式为
cosθ*dω也被称为投影立体角。因为它表示的就是立体角微分到x-z平面的投影。
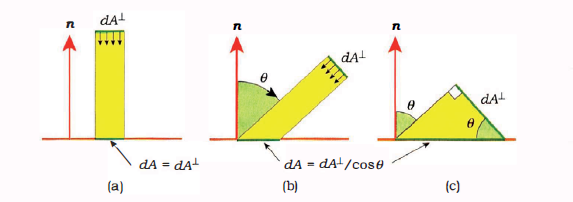
微分辐照功率密度:
现实世界中,最终进入到眼睛的光线都是经过多次反射或者光源直接发射达到眼睛的。根据生活经验可知,同样的光线照射到不同材质的物体上,眼睛看到的物体的颜色也是不相同的。这也给了人们一个启示那就是入射光和反射光是成一定映射关系的。这就是是BRDF(Bidirectional Reflectance Distribution Function)。之所以称为双向反射,是因为将如何光和反射光进行调换,函数不变,结果也是正确的。根据前面介绍的辐射率定义 L = d2Φ/(dA*cosθ*dω) ,对公式加入几个变量得
表示的是点 p 收到来自 ωi 方向的辐照率。公式左右两边乘以 cosθ*dωi 得
dEi ( p , ωi ) 表示的是辐照在微分立体角 dωi 所形成的圆锥且方向为 ωi 的辐射功率密度(如下图所示)。那么 p 点的辐射功率密度可以通过对 dEi ( p, ωi ) 进行有限积分得到即:
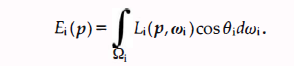 (6)
(6)
在现实生活中,测量某一点的辐照率是非常困难的,须保证光源正好覆盖测量仪开口立体角,大了该点会接受到比测量值更多的光照,导致测量值比实际值小,小了则与仪器的设计立体角不一致,可在实际中是基本做不到光源大小正好覆盖测量仪开口立体角的。而测表面的辐照度则简单得多,只要保证光源很小,而且没有来自其他方向的光干扰,这时候测到的辐照度就是平面上来自光源方向的微分辐照度dE。而测某一点的辐射率则非常简单只需要用仪器(B)从该方向对准该点就可以了。根据经验可知,现实世界的物体材质反射的辐射率和辐照功率密度是成正比的。而辐照功率密度可以通过类似如下的测量器就可以得到(光通量Φ除以传感器面积A就可以得到辐照功率密度E)。
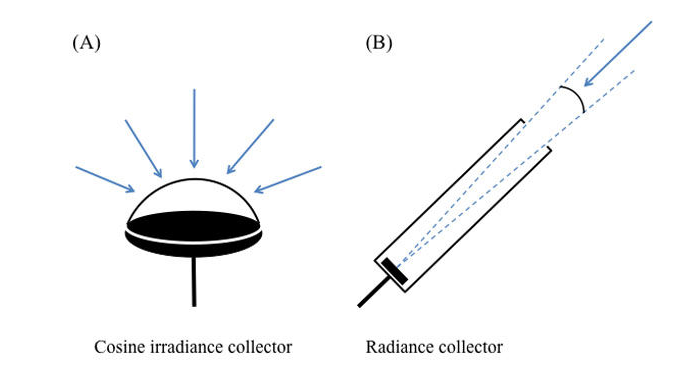
根据上述讨论可得得到等式:
fr( p, ωi, ωo )称为比例系数,也就是BRDF的分布函数。根据公式(5)可知
进而得到
BRDF有个单位即 sr-1 因为在分母中有个立体角。从式子(9)可知,BRDF是一个仅仅和点 p 已经入射和出射方向有关的函数。它的值可以是 0 到+∞,那什么时候BRDF值是无穷呢? 一个简单的例子那就是镜面反射。镜面的辐射率是等于辐照率的即 dLo ( p , ωo ) = Li( p, ωi )。由于式子(9)中含有微小分量 dωi 。所以 fr( p , ωi, ωo ) 值就是无穷。
反射辐射率
在 ωo 方向的反射辐射率是由在 p 点的上半球有限积分,积分表示是:
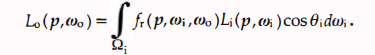 (10)
(10)由于对 p 点的上半球积分,所以公式又可以写成(球的立体角是4PI):
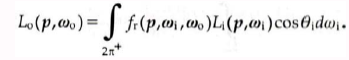 (11)
(11)这就是反射方程。它在射线追踪算法中扮演着重要的角色。因为式子(11)的右边的式子是射线追踪算法中每个碰撞点必须进行计算的量。至少对于纯反射材质是如此的,当然不包括光源。BRDF有以下几点属性:
1:互换性:互换 ωi , ωo 即 fr ( p, ωi , ωo ) = fr ( p, ωo , ωi ).
2:线性的:多个材质经常需要多个BRDF来模拟物体的反射属性,那么曲面上一点的总的反射辐射率就是来自不同材质物体的反射辐射率照射在曲面的p点的辐照率总和。(这也就式子(11)为什么是对点 p 的入射立体角进行积分的原因)
反射系数:
反射的辐射功率 和辐照功率的比值称为反射系数。有公式 Li ( p , ωi ) * cosθ*dωi = dEi ( p , ωi ) 和辐射功率密度定义得
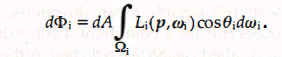 (12)
(12)同理可得
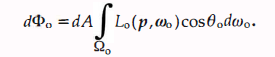 (13)
(13)将公式(8)dLo ( p , ωo )= fr(p, ωi , ωo ) * Li (p, ωi ) * cosθ*dωi 带入到公式(13)得
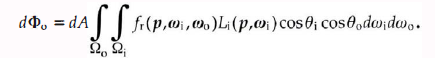 (14)
(14)那么反射系数 ρ ( p , ωi , ωo ) = dΦo /dΦi
展开得:
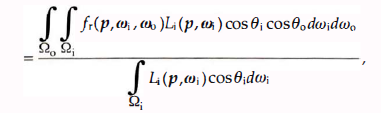 (15)
(15)根据现实物理规律可知,不存在能将入射光线全部反射的材质,任何材质肯定会吸收一些能量(转换成热能或者再辐射出去)。所以 ρ ( p , 2PI+ , 2PI+ ) < 1.
理想漫反射BRDF
通过讨论最简单的BRDF之一--理想漫反射将有助于我们对BRDF的理解。所谓理想漫反射就是在 p 的入射辐射功率被均匀的反射到各个方向。如下图所示:
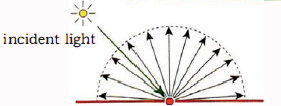 (15)
(15)理想漫反射模型也称为Lambert 反射。尽管显示中并不存在这种材质。但是漫反射模型是直接光照和间接光照模型的重要部分,因为该模型可以很近似的模型 平整粗糙的表面,比如纸张。对于Lamert反射来说,由于其反射的辐射量是各向同性的,所以 Lo ( p , ωo ) 是一个 ωo 无关的量。所以 Lo ( p , ωo ) 可以写成 Lr ,d(p)。那么此时公式(8)BRDF fr ( p , ωi , ωo ) 只可能是一个与 ωi 、ωo 无关的量。所以其也可以写成 fr , d(p),所以其可以从式子(8)中积分式提出得:
 (16)
(16)又因 fr ,d(p) = Lr , d(p) / Ei ( p, ωi ) ,要想 fr , d(p) 用反射系数ρ(d)来表示。ρ(d) = dΦo /dΦi = dA*Lr ,d(p) / (dA*Ei (p)) = Lr , d(p) * PI / Ei (p)。从而得
fr ,d(p) = Lr , d(p) / Ei ( p, ωi ) = ρ(d) / PI 。
为了对环境光进行模拟, 需要使用双向半球反射用ρhh表示。它表示的是半球内的辐射通量全部被反射到半球内,并且入射辐射通量是各向同性的,和空间无关的量。通俗的说入射辐射率在半球各向都是均匀的并不会随着位置的改变而变化。所以 Li ( p , ωi ) = Li 是一个常量。根据有以上前提条件,可以将 Li ( p , ωi ) 从积分式(8)中提取到积分项外,从而得到式子:
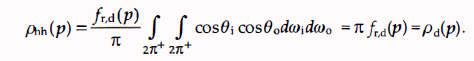 (17)
(17)[1] https://www.zhihu.com/question/24860046
本文转自:博客园 - JACAYANG,转载此文目的在于传递更多信息,版权归原作者所有。
原文链接:https://www.cnblogs.com/TobeYang/p/8387832.html
