机器学习的核心在于使用学习算法建立模型,对已建立模型的质量的评价方法和指标不少,本文以准确率(也称为精度)或判定系数(Coefficient of Determination)作为性能指标对模型的偏差与方差、欠拟合与过拟合概念进行探讨。偏差、方差、欠拟合、过拟合均是对模型(学习器)质量的判断和描述,训练集和验证集(测试集)上的准确率或判定系数得分为做出上述判断提供依据。
偏差(Bias)
偏差指预测输出与真实标记的差别,记为:

偏差度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。
方差(Variance)
方差指一个特定训练集训练得到的函数,与所有训练集得到平均函数的差的平方再取期望,记为:

方差度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。方差表示所有模型构建的预测函数,与真实函数的差别有多大。
偏差-方差示意图
偏差与方差的区别可用如下的靶标图来说明:
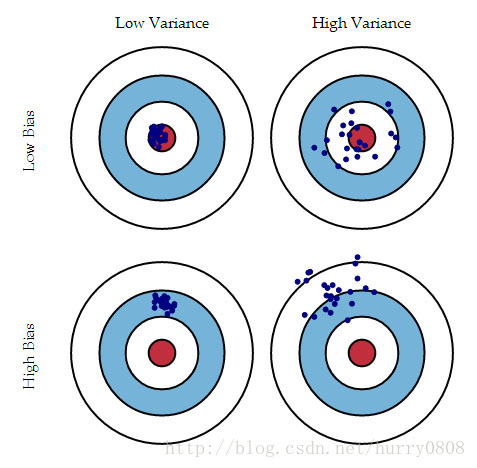
- 低偏差低方差时,是我们所追求的效果,此时预测值正中靶心(最接近真实值),且比较集中(方差小)。
- 低偏差高方差时,预测值基本落在真实值周围,但很分散,此时方差较大,说明模型的稳定性不够好。
- 高偏差低方差时,预测值与真实值有较大距离,但此时值很集中,方差小;模型的稳定性较好,但预测准确率不高,处于“一如既往地预测不准”的状态。
- 高偏差高方差时,是我们最不想看到的结果,此时模型不仅预测不准确,而且还不稳定,每次预测的值都差别比较大。
欠拟合(Under-Fitting)
模型不够复杂或者训练数据过少时,模型均无法捕捉训练数据的基本(或者内在)关系,会出现偏差。这样一来,模型一直会错误地预测数据,从而导致准确率降低。这种现象称之为模型欠拟合。
比如说,有的时候模型会过于复杂或者过于简单,以致于难以泛化新增添的数据;有的时候模型采用的学习算法并不适用于特定的数据结构;有的时候训练集本身可能有太多噪点或数据量过少,使得模型无法准确地预测目标变量。这些均是模型欠拟合的情况。
过拟合(Over-Fitting)
模型过于复杂或者没有足够的数据支持模型的训练时,模型含有训练集的特有信息,对训练集过于依赖,即模型会对训练集高度敏感,这种现象称之为模型过拟合。
欠拟合-过拟合与偏差-方差关系
通常来讲,模型欠拟合时,预测结果不准,偏差较大;但对于不同训练集,训练得到的模型都差不多(对训练集不敏感),此时的预测结果差别不大,方差小;以准确率作为性能指标,模型的训练集得分及验证得分均会比较低;模型复杂度可能低、训练集数据量可能少。模型过拟合时,模型含有训练集的信息,预测的准确度一般不高,偏差较大;模型对训练集敏感,在与总体同分布的相同大小的不同训练样本上训练得到的模型,在验证集上的表现不一,预测结果相差大,方差大;由于模型含有训练集的信息,此时的训练得分很高,但验证得分不高(偏差大);模型复杂度高、训练集数量大。
上述关系如下表所示:
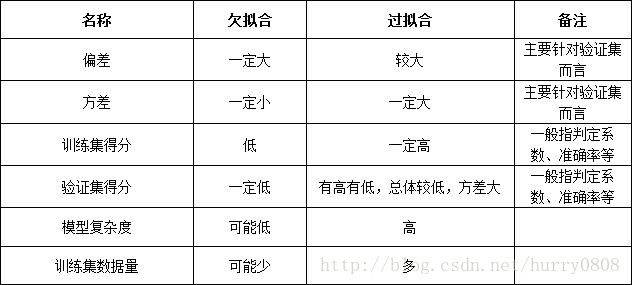
偏差-方差、欠拟合-过拟合实例分析
下图是决策树回归模型在不同最大深度参数设置时的学习曲线(learning_curve),展示了模型受最大深度参数的影响,训练得分、验证得分是模型在训练集、验证集上的判定系数(Coefficient of Determination,也称R^2,含义与准确率类似,值越大说明模型的拟合优度越好,预测越准确)值。
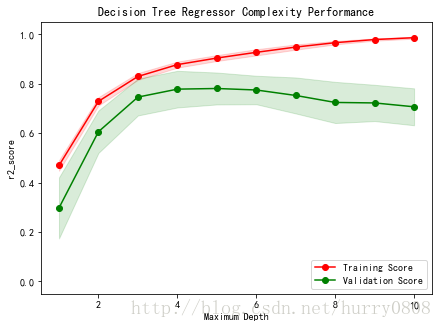
从图中可以看出:
1. 当模型以最大深度 1训练时,训练得分(约0.45)及验证得分(约0.3)都很低,说明模型的预测出现了很大的偏差,模型欠拟合。
2. 当模型的最大深度不断增大到10的过程中,训练得分呈上升趋势并最终约等于1;验证得分在最大深度为4处达到最大,之后呈下降趋势且与训练得分差距逐渐上升达到最大,说明模型过拟合,方差很大;最大深度为10时,训练得分与验证得分距离最大,训练得分曲线及验证得分曲线无趋于一致的收敛趋势,说明此时训练得到的模型质量较差,不能用于预测。
模型的偏差-方差折衷
一般来说,偏差与方差是冲突的,这称之为偏差-方差窘境(Bias-Variance Dilemma),也就是说,让偏差和方差都达到最小的模型是不存在的,模型只能在偏差和方差中取折衷,如下图所示:
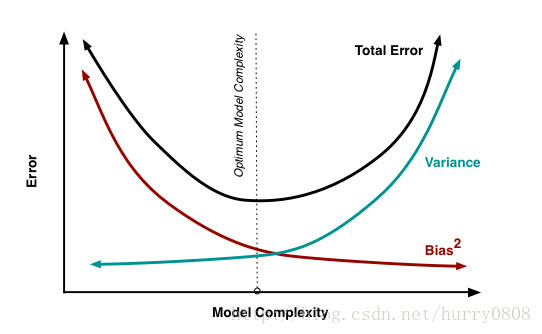
从图中可以看出,开始时,模型比较简单且训练不足,此时模型的拟合能力较弱(欠拟合),对训练集的扰动也不敏感,偏差主导了模型的泛化错误率(Error轴);随着更多参数、更多训练数据等加入到模型,模型的复杂度在提高,其拟合能力也在提升,偏差逐步下降,同时方差开始上升,但此时有可能获得偏差、方差都比较低的模型,即偏差-方差折衷后的最优模型;随着模型的复杂度进一步提高,且训练程度充足后(训练数据自身的、非全局的特性很可能被模型学到),模型的拟合能力已经非常强,训练数据的轻微扰动都会导致模型发生显著变化,进而导致其预测能力时好时坏,但总体低于最优状态,此时方差主导了模型的错误率,模型过拟合。
参考: http://scott.fortmann-roe.com/docs/BiasVariance.html
来源:CSDN,作者:Felix_YU_Q ,转载此文目的在于传递更多信息,版权归原作者所有。
原文:https://blog.csdn.net/hurry0808/article/details/78148756






