我们知道,人类在发展、成长、生活的过程中积累了很多的经验。通过定期的对这些经验进行总结,获得了一些规律,这就叫“归纳”。利用这个“归纳”出来的“规律”,对类似的情况进行决策判断,从而指导我们的行动,这就是“演绎”。
例如人类通过观察季节、农作物生长的变化,总结出历法、四季、24节气等规律来指导农业生产,这样,每到新的一年,我们就知道要春播,夏种,秋收,冬藏。当然,还有一些谚语像“朝霞不出门,晚霞行千里”,“春捂秋冻”等,也是对经验进行归纳总结出来的规律,并演绎指导我们春天要多穿衣服,秋天少穿衣服等等。
用一张图表示就是:
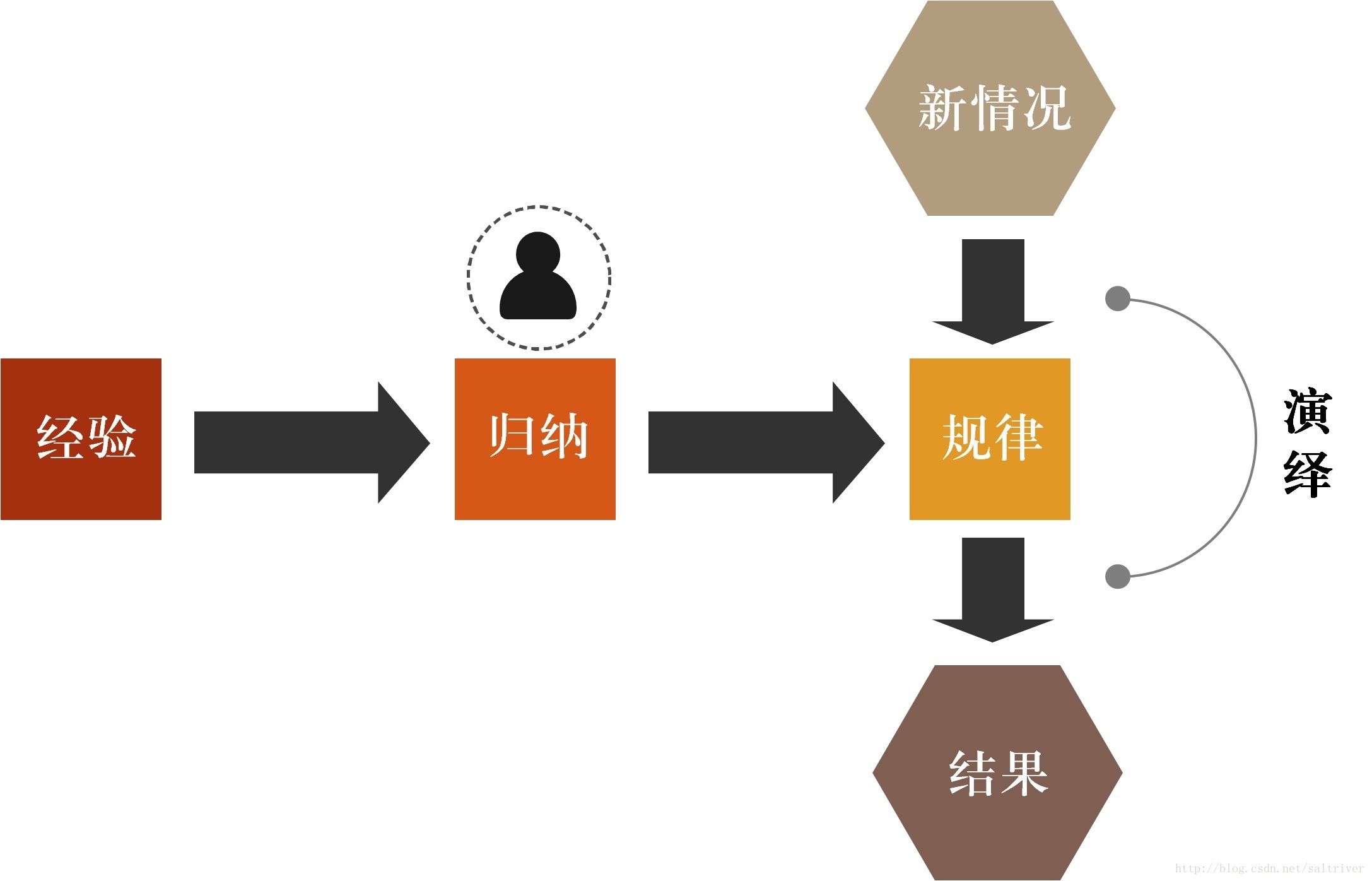
以前提过:机器学习就是让计算机学会利用过往的经验完成指定任务。其工作原理与人类的归纳演绎过程是一致的,也就是说:
机器学习只不过是在计算机中对人类归纳演绎过程进行的模拟。
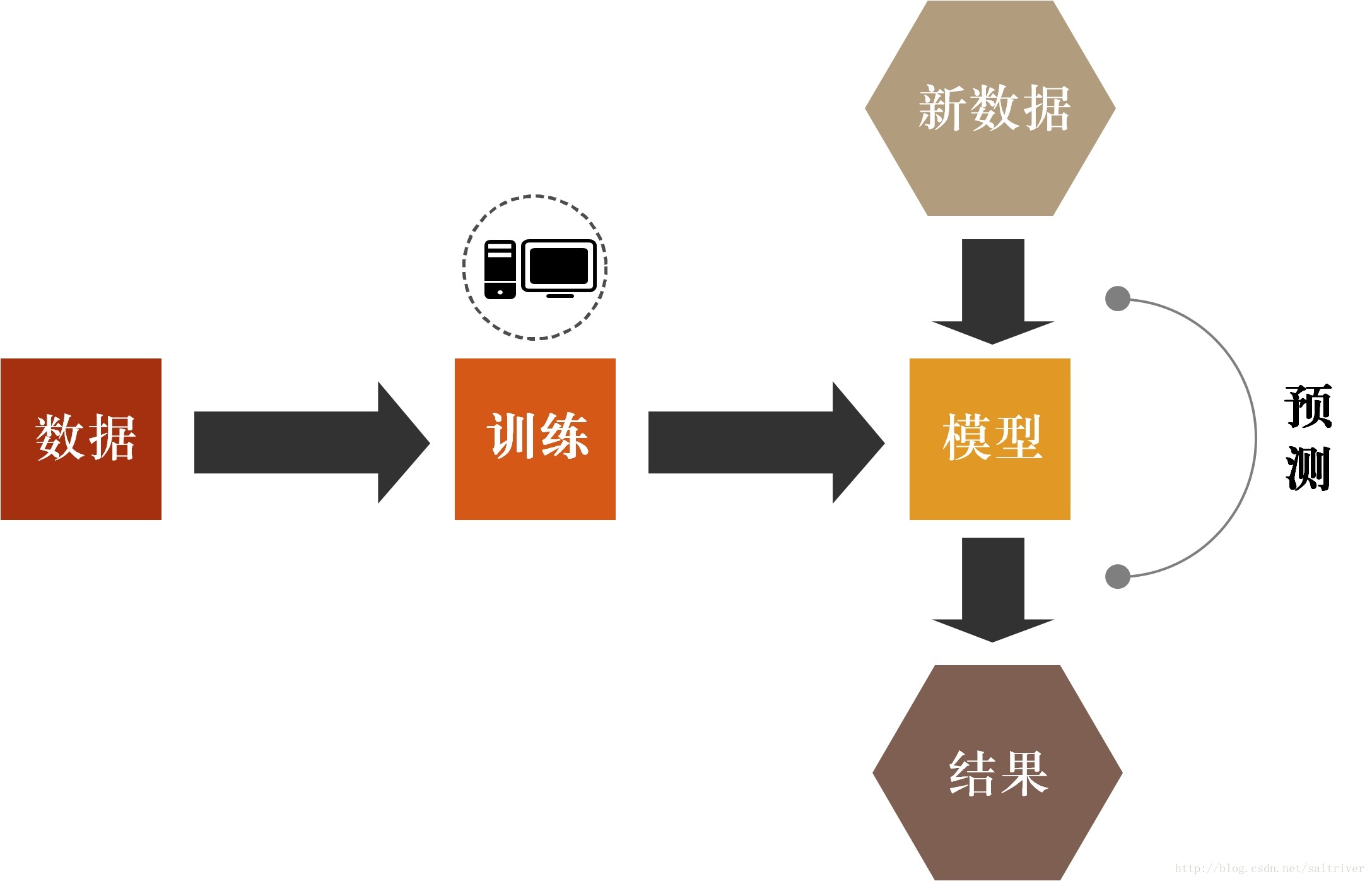
对比上面2张图,是不是一样的。对于机器学习,过往的经验就是存储下来的数据,因为有很多数据,所以称为数据集(data set),通过对这些数据进行训练(training)或者学习(learning),这两种叫法都可以,对应的是人类的“归纳总结”,然后得到一个模型(model),对应人类的是“规律”,然后对于一个新数据/新情况,通过这个模型来预测(predict)其结果,对应人类的是“演绎”。
这就是机器学习的工作原理。首先,我们需要有存储的历史数据。然后,我们对这些数据通过机器学习算法进行处理,这个处理的过程叫做训练。再然后我们通过训练得到一个模型。最后根据这个模型,我们可以输入新数据,得到预期的结果,这个过程叫做预测。以上就是机器学习的全过程。我把它称之为:
一个数据集,一个模型,两个过程
其中训练这个过程是核心所在,机器学习所有的精华和主要内容都在这个过程中。
我们举个例子说明下。假设你是一家大型互联网公司的人力资源经理,每年都要招聘大量的程序员。你手头上有历年来公司招聘的录用数据,我们假设应聘者能否录用只与笔试成绩和面试成绩这2项有关。
数据如下:
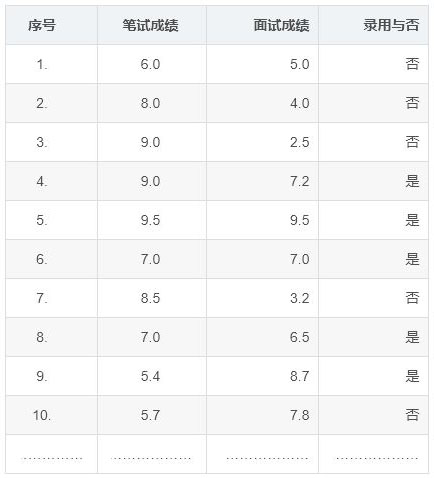
这里有几个概念术语需要说明下。
- 这组记录的数据集合称为“数据集(data set)”。
- 数据集中每一条记录称为一个“样本(sample)”或叫“示例(instance)”。
- 样本中的结果信息“录用与否”称为“标记(label)”,好理解的话你可以叫它“目标结果”。
- 描述样本的“笔试成绩”、“面试成绩”称为“特征(feature)”或“属性(attribute)”,叫“特征”也行,叫“属性”也行,都可以。
- 属性(或者叫特征)的个数称为“维度(dimensionality)”,上面这个数据集就是2个维度,因为只有“笔试成绩”、“面试成绩”这2个属性。
我们把数据集用图表的形式绘制出来。
如下图所示:
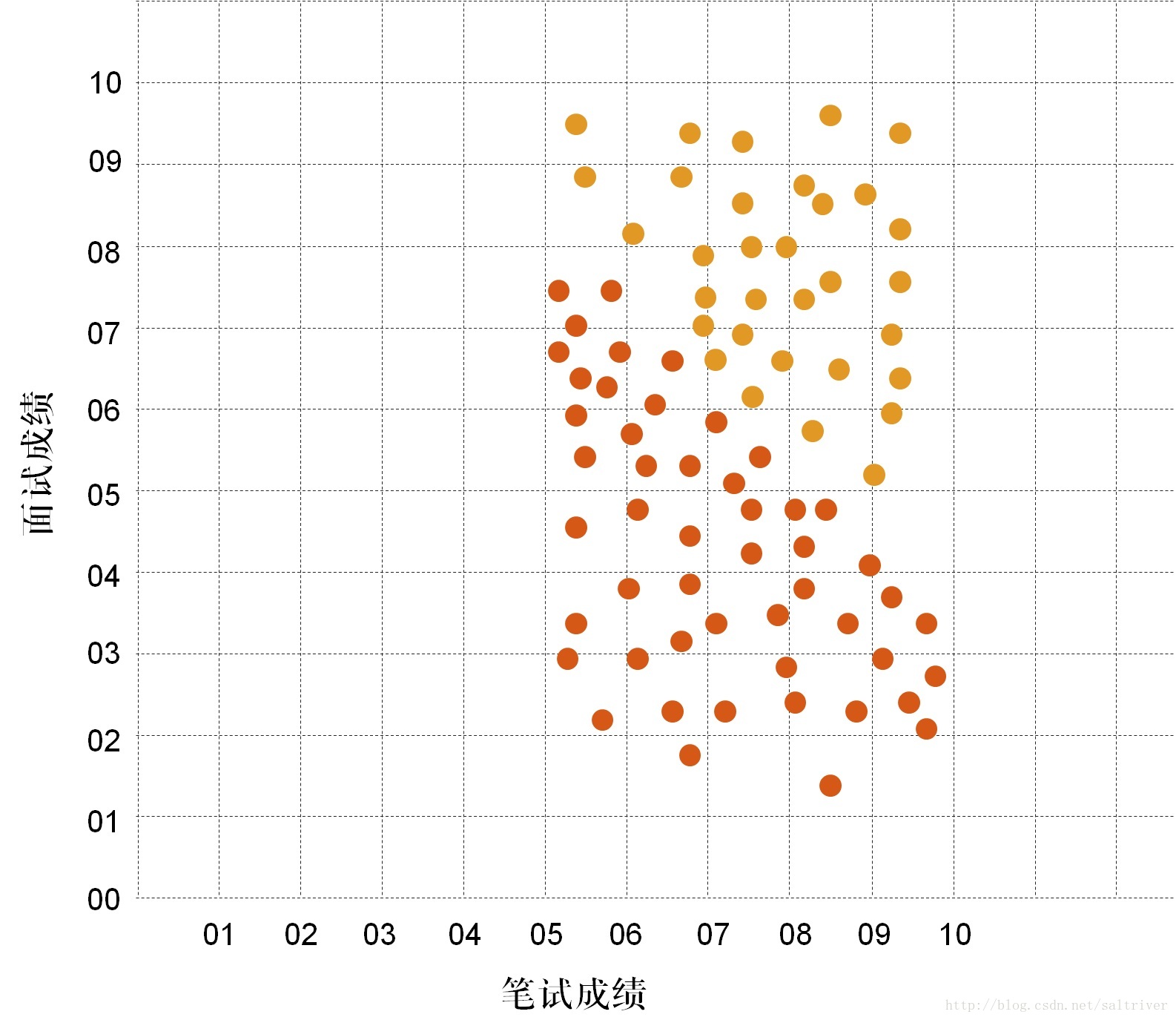
红色的点是未录用的数据,橙色的点是录用的数据。我们仔细观察下这些数据,发现好像有一条直线把这些数据分开了。如下图所示:
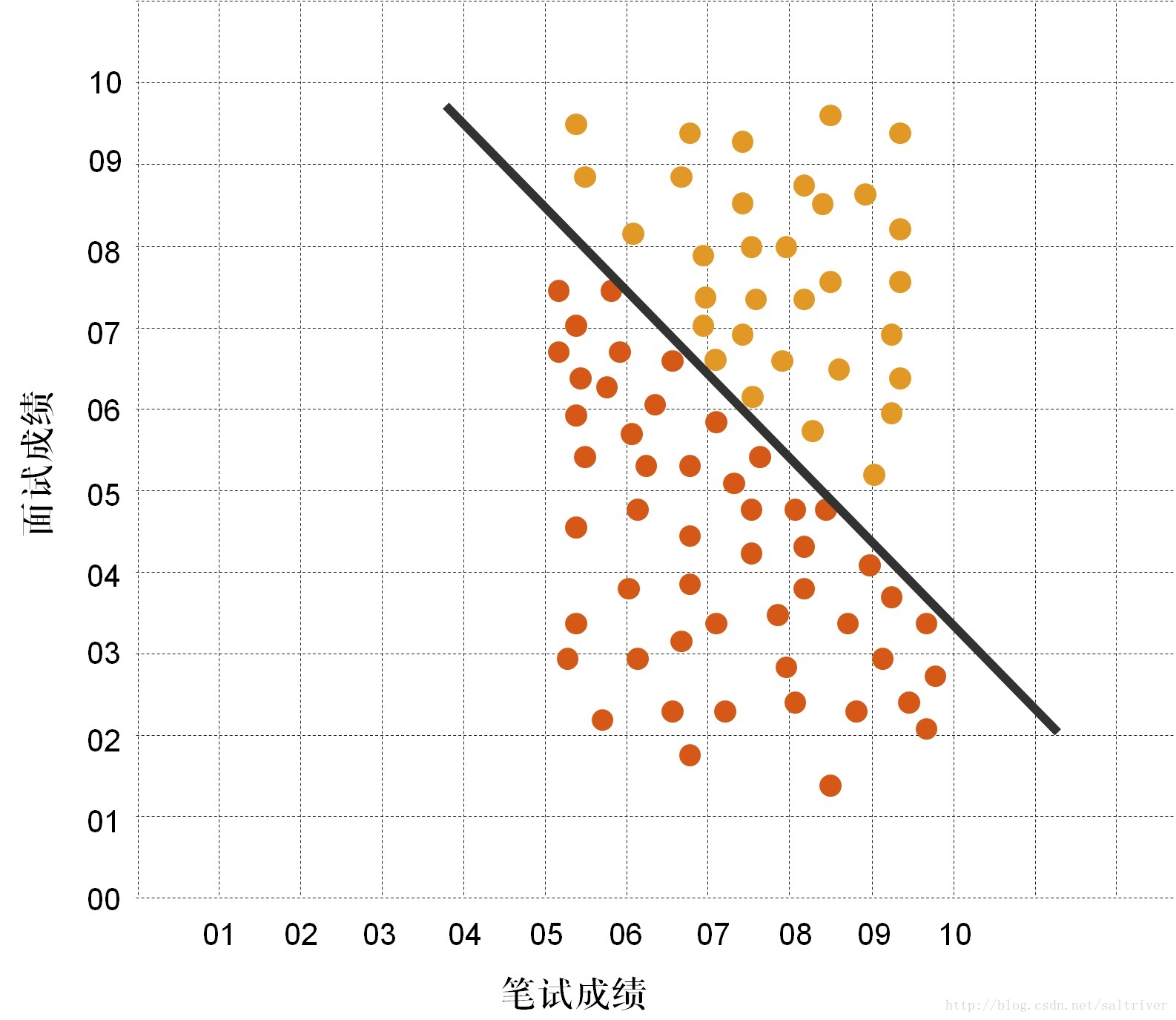
如果机器学习能找出这条直线,那么得到新的应聘者笔试成绩和面试成绩后,如果新数据落在直线左边,就可以决策不录用,如果新数据落在直线右边,就决策录用。这条能辅助决策的直线,我们称之为“决策边界”或叫“决策面”。为什么又叫“决策面”,因为三维空间中,决策边界可能是个平面,如果是更高维度的空间,决策边界可能是个超平面。
看到这,有人就会说,这还用得着机器学习啊?这个图我看一眼就能看出来这条直线。确实,这个例子很简单,人用肉眼就能判断。但是,我们还是要用到机器学习。为什么?
首先,计算机的强项在于计算和批量处理。你看,你能写出这条直线的方程吗,中学阶段我们学过直线方程为y = kx + b,那这里的k和b各是多少?你很难马上手工算出来吧。即使你能算出来,如果你需要处理5万个样本数据,决策今年的3000个应聘者的录用与否,你能手工一个个的处理吗?
其次,这个决策边界不一定是一条直线,可能是多条直线,甚至可能是曲线。更多的可能性是根本无法描述。在这个例子中,样本数据只有2个属性,笔记成绩和面试成绩,这恰好是2个数值数据,现实中样本数据可能是数值数据,也有可能是类别数据,例如这个数据集再添加应聘者的毕业院校、所学专业2个属性,有这样4个属性的样本数据的决策边界就无法直观描述了。
一般的数据维度都高于2维,甚至4维、5维……。在3维数据中看出决策边界就很难了,而4维及以上维度根本就画不出图来,生活在3维空间的我们不可能感知4维及以上的空间,也就是说你不可能感知到超平面。
所以,这也是我们需要机器学习的主要原因。让我们看看怎样找出这条直线。我们假设这个直线为y=kx+b,先随机设定参数值k=1,b=1。
如下图所示:
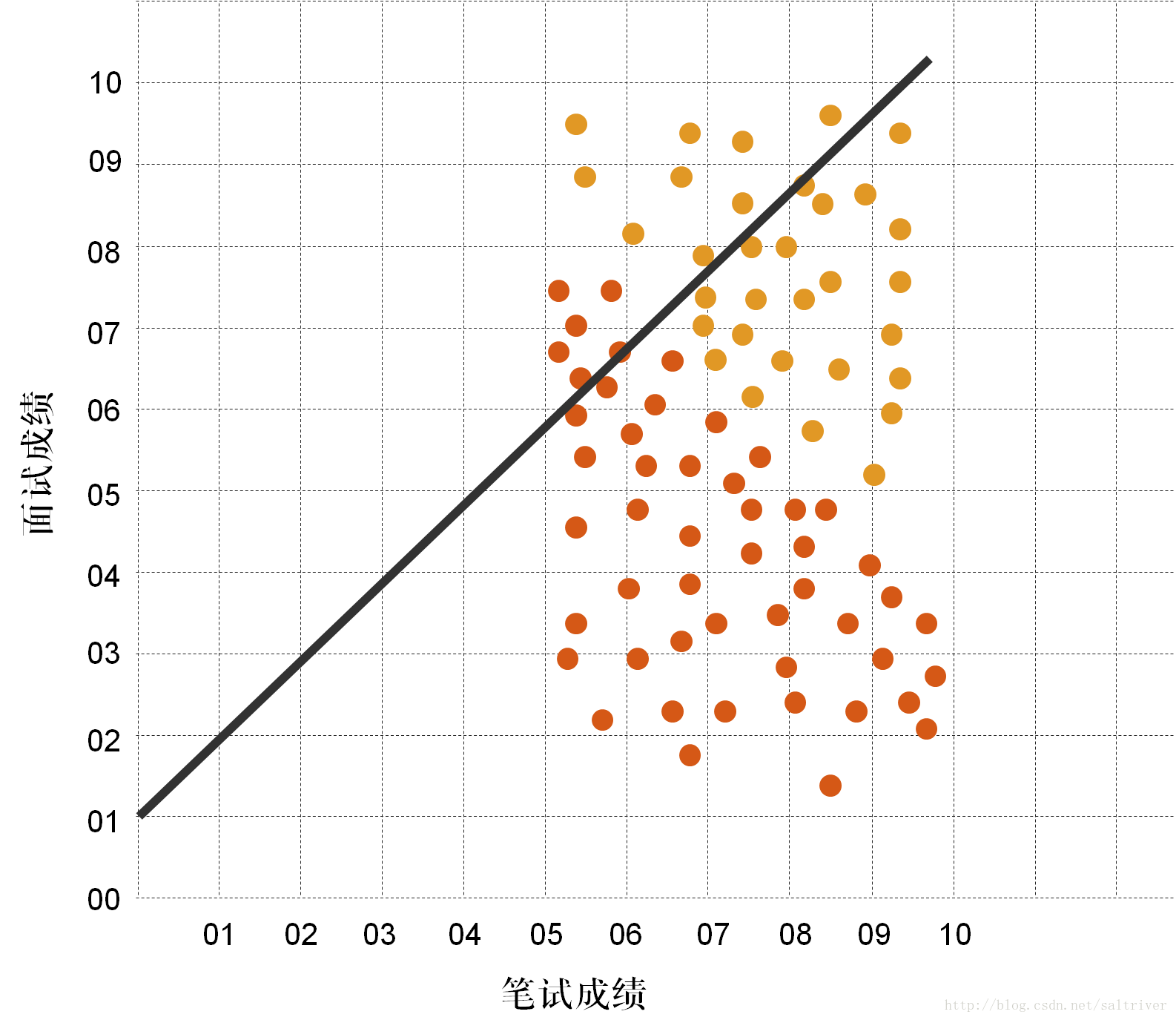
我们将数据集中的训练样本数据与这条直线比对,发现效果很差,大部分都分错了。那么,我们调整下k,b的值。见下图,这次效果好多了,但还是差不多错了一半。
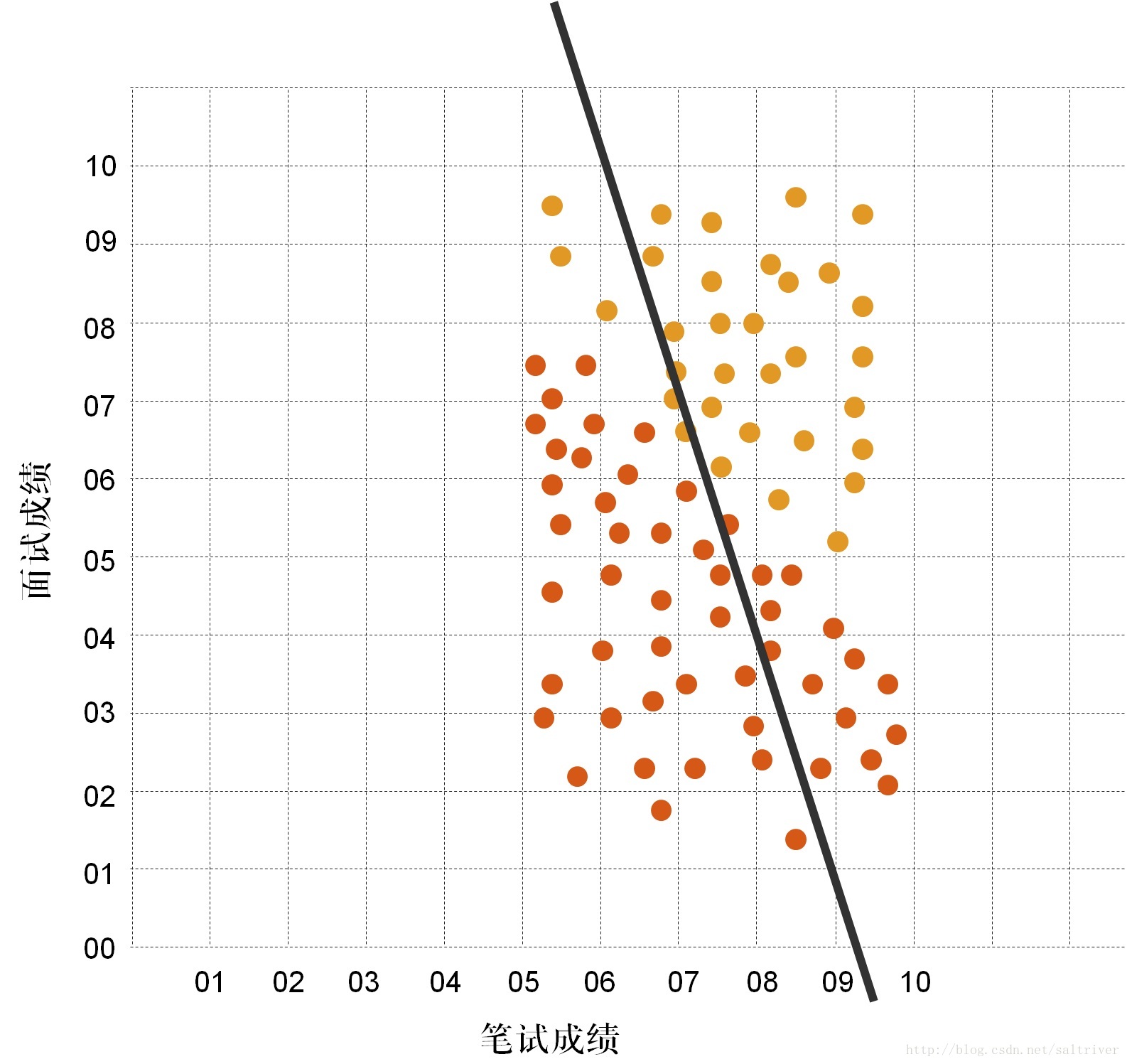
然后再调整下k,b的值。见下图,这次效果又好多了,接近最优解了。
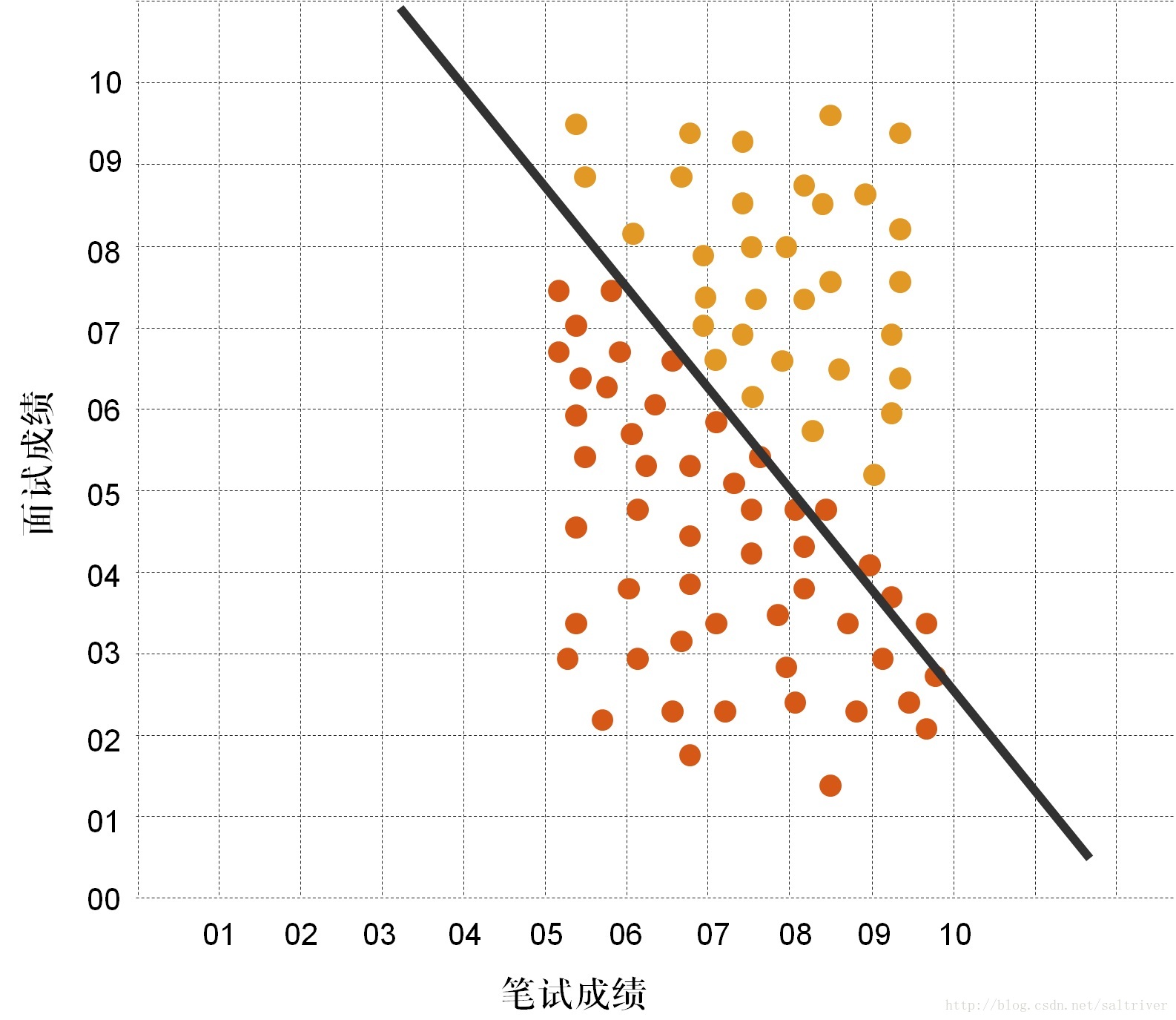
就这样不断找下去,就可以找到这条直线了。那么问题来了,这跟不断试错有什么区别?有区别的,因为这里调整k,b的值是有方向的调整,而不是随机的调整,这其实是一个求解k,b参数最优化的问题,对于最优化问题,这本身就是一个大的领域。常用的最优化问题求解算法有梯度下降法、牛顿法、遗传算法、粒子群算法等,在机器学习中梯度下降法用的较多。需要注意的是这里的梯度下降法、遗传算法等不是我们通常说的机器学习算法,而是在大的机器学习算法过程中,用于求解像k,b这些参数的最优化问题求解算法。而逻辑回归、决策树、朴素贝叶斯、支持向量机、神经网络等,才是我们通常说的机器学习算法,这个以后在讲具体的机器学习算法时再谈。
在求解出这条直线后,也就是机器学习训练出一个模型后,那么现在,有一个应聘者的笔试成绩是6.5,面试成绩是7.2。你认为应该是录用还是不录用呢?直接判断点(6.5,7.2)在这条直线的左边还是右边就可以了。
此外,很多时候,我们需要了解和测试机器学习的效果,并评估其精确度,这就是预测精确度,一般用百分比表示。这种情况下我们通常准备2套独立的数据集,或者将一个数据集分割成2部分,例如上面的数据集,假设有5万个样本。我们采用前4万个样本进行训练。那么这4万个样本的集合我们称为“训练集”。剩下的1万个样本用于对训练出来的模型进行测试,这1万个样本的集合称为“测试集”。测试后获得的预测结果与测试集中的实际结果信息进行比对,就可以得出机器学习的精确度。例如测试集中的1万个样本预测的结果与实际结果比对,匹配一致的有9500个,不匹配的有500个,这样我们就知道训练出来的模型的大致效果了。
至于为什么要分成训练集和测试集,其实很好理解,从一些现象推导出的任何严谨结论,都需要进行验证,这也是科学方法论遵循的基础。就像大科学家爱因斯坦提出的质能方程E = MC2 ,也需要通过进行核试验来验证其正确性。
来源:CSDN,作者:saltriver,转载此文目的在于传递更多信息,版权归原作者所有。
原文链接:https://blog.csdn.net/saltriver/article/details/69808434






