本文阐述深度学习中使用的一些初始化技术。任何甚至没有机器学习背景的人都必须知道我们需要学习权重或超参数来制作模型。这些参数控制着我们的算法在看不见的数据上的表现。要学习模型,我们需要初始化参数,应用损失函数然后对其进行优化。
如果你已经构建过任何机器学习算法,必须听说过我们需要"随机"初始化我们的权重作为起点然后开始学习过程。随机这个词本身就很模糊。我们将看到这个随机背后的实际内容以及不同的初始化技术。
零启动
这是通过将所有权重等于零来初始化权重的最简单方法之一。现在让我们使用一个简单的双层网络可视化这种技术的含义。
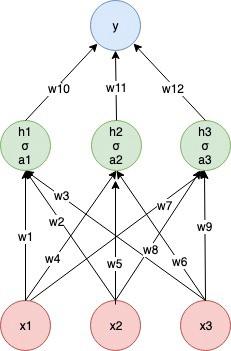
由于我们设置了所有权重,即w = 0,我们可以很容易地看到在前向传递期间:
a1 = w1 * x1 + w2 * x2 + w3 * x3,h1 = g(w1 * x1 + w2 * x2 + w3 * x3) a2 = w4 * x1 + w5 * x2 + w6 * x3,h2 = g(w4 * x1 + w5 * x2 + w6 * x3) a3 = w7 * x1 + w8 * x2 + w9 * x3,h3 = g(w7 * x1 + w8 * x2 + w9 * x3) y = g(h1 * w10 + h2 * w11 + h3 * w12)
很清楚地看到a1 = a2 = a3 = 0并且h1 = h2 = h3。- > (1)
现在让我们看看反向传播会发生什么
∇ W1 =∂L(W)· /∂w1=∂L(W)· /∂L(Y)· *∂L(Y)· /∂L(H1)· *∂L(H1)· /∂L (a1)̇*̇x1 ∇ W4 =∂L(W)· /∂w4=∂L(W)· /∂L(Y)· *∂L(Y)· /∂L(H2)· *∂L(H 2)· /∂L (a2)̇*̇x1 ∇ W7 =∂L(W)· /∂w7=∂L(W)· /∂L(Y)· *∂L(Y)· /∂L(H3)· *∂L(H3)· /∂L (a3)̇*̇x1 因此我们可以看到∇w1=∇w4=∇w7(从1),类似地∇w2=∇w5=∇w7和∇w3=∇w6=∇w9
从上面的论证中,我们可以看到,在每一步中,权重的变化是相同的。因此,隐藏层中的所有节点都在学习与输入相同的参数,这导致冗余并使我们的网络不那么灵活,因此不太准确。这也称为对称问题。
因此,零初始化不是一种好技术。
使用相同的随机值进行初始化
在这种技术中,我们用相同的随机值初始化所有权重。我希望你已经遇到了这种技术的问题,因为它与零初始化非常相似,我们只是使用了一个随机值,但同样的问题仍然存在,因为权重的更新将再次以相同的顺序。
因此,也不推荐使用这种技术。
使用小的随机值进行初始化
在这种技术中,我们从具有均值0和方差1的单变量"高斯"(正态)分布中随机初始化所有权重,并将它们乘以10的负幂以使它们变小。我们可以使用numpy在Python中执行此操作,如下所示
W = np.random.randn(input_layer_neurons,hidden_layer_neurons)* 0.01
通过绘制梯度的值,期望Normal曲线类似于:
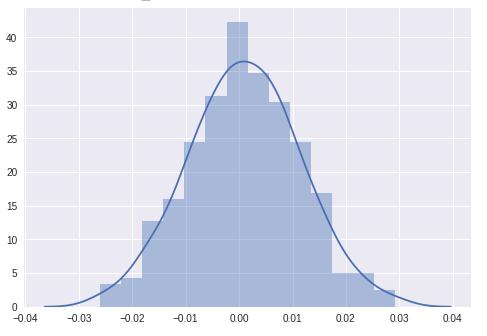
现在,我们将运行学习算法,看看分布如何随着不同的eopch而变化
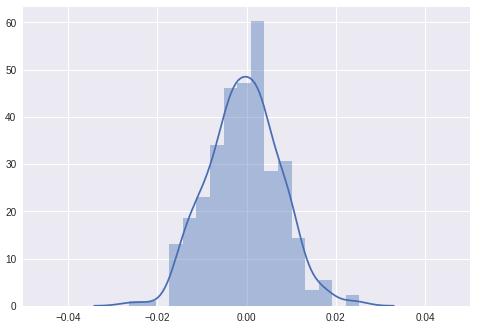
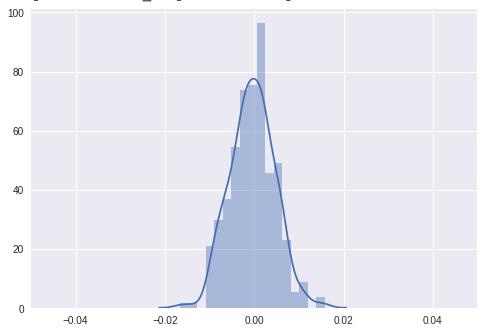
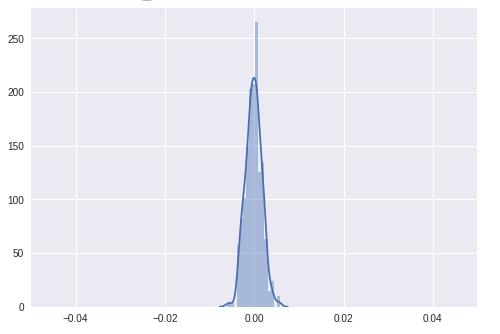
从上面的图中,可以很容易地看出方差正在减小,梯度饱和到0。这被称为梯度消失问题。人们还可以看到这一点,因为每个梯度是由导数的乘法链获得的,并且每个值远小于1,因此梯度消失为零。
当这些梯度向前传播时,神经元具有S形激活,神经元的输出接近0.5,如sigmoid(0)= 0.5,而在tanh的情况下,它将与梯度图中心相同。
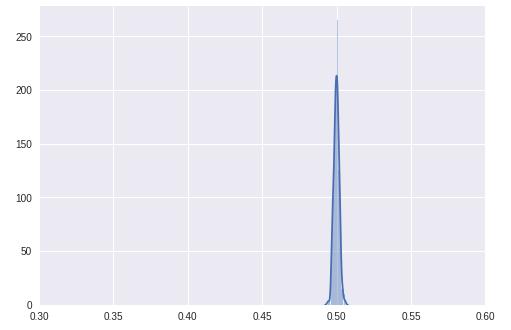
因此,我们可以得出结论,如果我们采用小的随机值,则梯度在重复链增殖时消失,并且在sigmoid的情况下神经元饱和到0.5的值,在tanh的情况下为0。因此我们不能使用小的随机值作为初始化。
使用大随机值进行初始化
我们刚看到,在随机值较小的情况下,梯度消失。现在让我们看看当我们用大的随机值初始化权重时会发生什么。我们可以使用numpy在Python中执行此操作,如下所示
W = np.random.randn(input_layer_neurons,hidden_layer_neurons)
当我们将权重初始化为大值时,绝对和WiXi将非常大,并且在前向传递期间神经元会达到极限,如下所示。

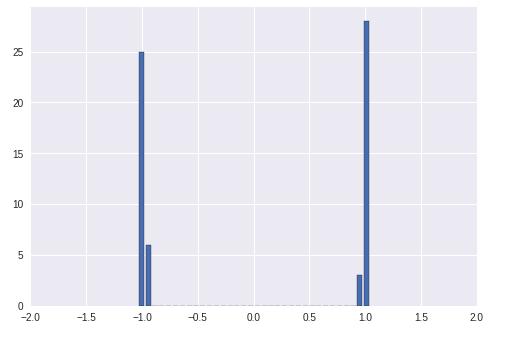
下图显示,在饱和时,S形的导数消失为0。也可以对tanh进行类似的论证。

现在,当我们通过网络反向传播时,导数将倾向于零,因此在这种情况下梯度也会消失。因此,如果您认为我们已经初始化了较大的权重,因此渐变会爆炸而不是消失,那么由于大值饱和而不是sigmoid和tanh作为激活的情况。
上述两个论点向我们表明,在两种情况下,要么将权重初始化为较小的值,要么将较大的权重倾向于消失。在较小的值中,梯度因重复的链式乘法而消失,而在大的情况下它会消失,因为导数本身变为零。因此它们都无法使用。
在尝试任何新方法之前,我们将尝试建立一些直觉,为什么它在数学上发生。
让我们谈谈你的神经网络的输入,你必须知道我们在输入网络之前规范化我们的输入。为了论证,让我们考虑我们的输入来自均值0和方差1正态分布。我们将来自上述网络的a1的等式推广为n输入
a1 = w1 * x1 + w2 * x2 + w3 * x3 + ...... + + wn * xn
现在我们将计算a1的方差
Var(a1)= Var(ΣWiXi) =ΣVar(WiXi) =Σ[(E [Wi])²Var(Xi)+(E [Xi])²Var(Wi)+ Var(Wi)Var(Xi)]
考虑输入和权重,因为零均值前两个项将抵消。
=ΣVar(Wi)Var(Xi)
由于所有WiXi都是相同分布的,我们可以写
= NVAR(Wi)VAR(Xi)
我们发现Var(a1)=(nVar(Wi))Var(Xi)或者我们可以说我们的输入Xi被缩放到(nVar(Wi))次方差。一些更多的数学,我们将能够证明第k个隐藏层,Var(ak)的方差=([(nVar(Wi))] ^ k)Var(Xi)。
这个陈述的物理意义在于,隐藏层中的任何神经元现在可以改变输入的变化n倍(这也是前一层输入的n倍方差),或者如果我们绘制分布,我们将发现Var(ak) )比Var(Xi)更广泛传播。
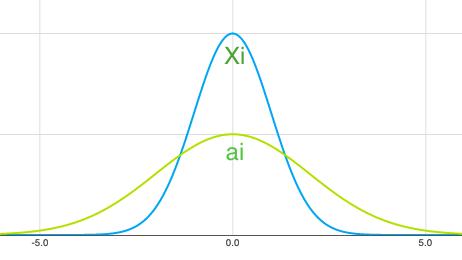
现在让我们看看(nVar(Wi))^ k在不同的值(nVar(Wi))会发生什么
- 如果(nVar(Wi))>> 1,则渐变会爆炸
- 如果(nVar(Wi))<< 1,渐变将消失
因此,我们的工作是限制(nVar(Wi))= 1,以避免爆炸或消失梯度的问题,并且方差的传播将在整个网络中保持不变。
(nVar(Wi))= 1 Var(Wi)= 1 / n
因此,如果我们将从高斯分布获得的权重缩放为均值0和方差1到1 / √n,那么我们就得到了
nVar(Wi)= nVar(W /√n) = n * 1 / n Var(W) = 1
因此,最后我们的任务是从方差分布初始化权重,方差为1并将其缩放为1 / √n,其中n是前一层中的节点数。在Python中,我们可以使用
W = np.random.randn(input_layer_neurons,hidden_layer_neurons)* sqrt(1 / input_layer_neurons)
这也称为Xavier初始化或Glorot初始化
在ReLU激活函数的情况下,我们乘以√2 / √n以考虑对任何方差没有贡献的负半(x <0)。这也称为He初始化。
W = np.random.randn(input_layer_neurons,hidden_layer_neurons)* sqrt(2 / input_layer_neurons)
Xavier初始化的一些其他变体包括除以输入层神经元和当前隐藏层神经元的数量之和。即
Var(Wi)= 2 /(input_layer_neurons + hidden_layer_neurons)
像Keras这样的高级API也使用Glorot Initialisation,尽管底层分布可以是Gaussian或Uniform。
总结一下
如果你能够跟随一些令人难以置信的数学。真棒。所以我们首先看到我们不能使用零或相同的初始化,因为所有权重往往以相同的幅度更新,因此阻碍了学习过程。此外,我们看到如果我们将权重初始化为太小或太大的值,那么它们倾向于饱和并且梯度下降到0。因此需要初始化权重,使得隐藏层中神经元之间的变化保持不变并且Xavier初始化允许我们这样做,因此它是任何网络初始化的最明显选择。
有一些技术,例如批量归一化,它会在将每个隐藏层传播到下一层之前对其进行标准化,就像我们在将它们输入网络之前一样。这减少了对权重初始化的强烈依赖,可使我们对初始化粗糙一点也没关系。
本文转自:今日头条 - AI火箭营,转载此文目的在于传递更多信息,版权归原作者所有。






