离散卷积是两个离散序列之间按照一定的规则将它们的有关序列值分别两两相乘再相加的一种特殊的运算。
离散单位脉冲和单位阶跃信号
离散状态下的单位脉冲信号表达式如下所示:
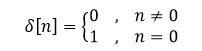
离散状态下的单位阶跃序列表达式如下所示:
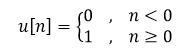
上述两式画成函数图像就是:
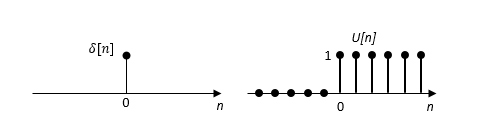
任意离散时间信号
任意离散时间信号可以看成是由离散时间单位脉冲的移位加权单位脉冲组成。用x[n]表示任意离散时间信号,将移位单位脉冲信号与x[k]相乘可得如下结果,x[k]为x[n]序列中的某个值:
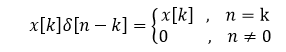
将该表达式扩展到整个x[n]中,并将它们相加有:

根据单位脉冲表达式可以很容易看出,对全部的n值来说,每个n值中的表达式只有一个项是非零值,而这个非零值就是x[n]。将上式写为累加和形式可以得出如下式子,这就是离散时间单位脉冲序列的筛选性质:
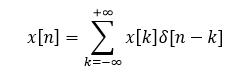
卷积和
现在假设x[n]是某线性时不变系统的输入,由x[n]的表达式可以将其表达为一组加权移位单位脉冲的线性组合。将hk[n]记为该线性系统对移位单位脉冲δ[n-k]的响应,根据线性系统的叠加性质,该线性系统对输入x[n]的响应y[n]就是这些基本响应的加权线性组合。那么根据上述可以得出y[n]表达式如下所示,其中x[k]为加权单位脉冲,相当于权因子。
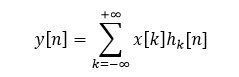
线性系统的时不变性意味着一个时不变系统对移位单位脉冲的响应就是未被移位的单位脉冲的响应的移位,因此上式可以写为:
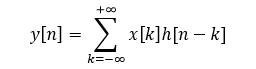
这个结果就称之为卷积和,并且式右边的运算称为x[n]和h[n]卷积,并用符号记作:
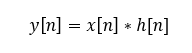
本文转自:博客园 - MagicianY.L,转载此文目的在于传递更多信息,版权归原作者所有。