前言
转置卷积又叫反卷积、逆卷积。不过转置卷积是目前最为正规和主流的名称,因为这个名称更加贴切的描述了卷积的计算过程,而其他的名字容易造成误导。在主流的深度学习框架中,如TensorFlow,Pytorch,Keras中的函数名都是conv_transpose。所以学习转置卷积之前,我们一定要弄清楚标准名称,遇到他人说反卷积、逆卷积也要帮其纠正,让不正确的命名尽早的淹没在历史的长河中。
我们先说一下为什么人们很喜欢叫转置卷积为反卷积或逆卷积。首先举一个例子,将一个4x4的输入通过3x3的卷积核在进行普通卷积(无padding, stride=1),将得到一个2x2的输出。而转置卷积将一个2x2的输入通过同样3x3大小的卷积核将得到一个4x4的输出,看起来似乎是普通卷积的逆过程。就好像是加法的逆过程是减法,乘法的逆过程是除法一样,人们自然而然的认为这两个操作似乎是一个可逆的过程。但事实上两者并没有什么关系,操作的过程也不是可逆的。
下面我们将一点一点的抽丝剥茧来深刻的理解转置卷积的思想。
普通卷积(直接卷积)
普通的卷积过程大家都很熟悉了,可以直观的理解为一个带颜色小窗户(卷积核)在原始的输入图像一步一步的挪动,来通过加权计算得到输出特征。 如下图。
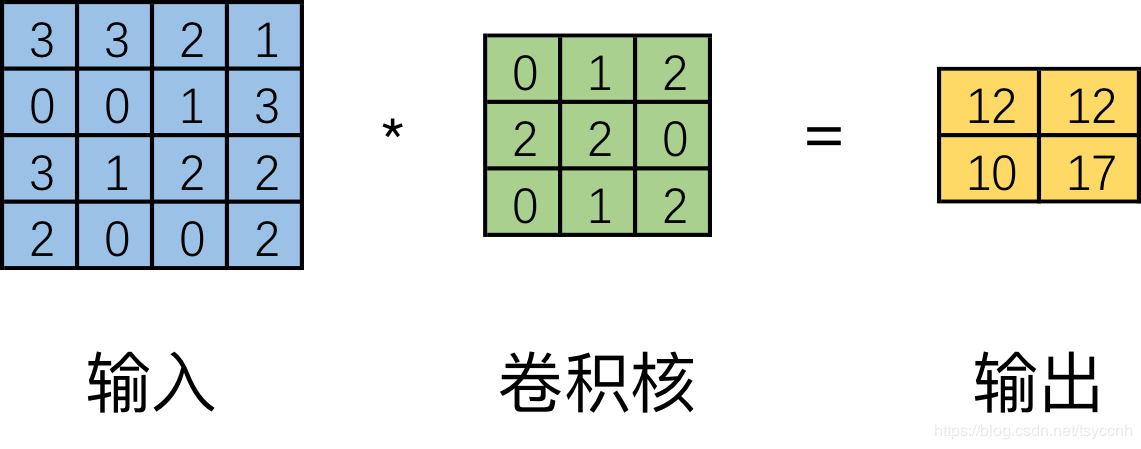
但是实际在计算机中计算的时候,并不是像这样一个位置一个位置的进行滑动计算,因为这样的效率太低了。计算机会将卷积核转换成等效的矩阵,将输入转换为向量。通过输入向量和卷积核矩阵的相乘获得输出向量。输出的向量经过整形便可得到我们的二维输出特征。具体的操作如下图所示。由于我们的3x3卷积核要在输入上不同的位置卷积4次,所以通过补零的方法将卷积核分别置于一个4x4矩阵的四个角落。这样我们的输入可以直接和这四个4x4的矩阵进行卷积,而舍去了滑动这一操作步骤。
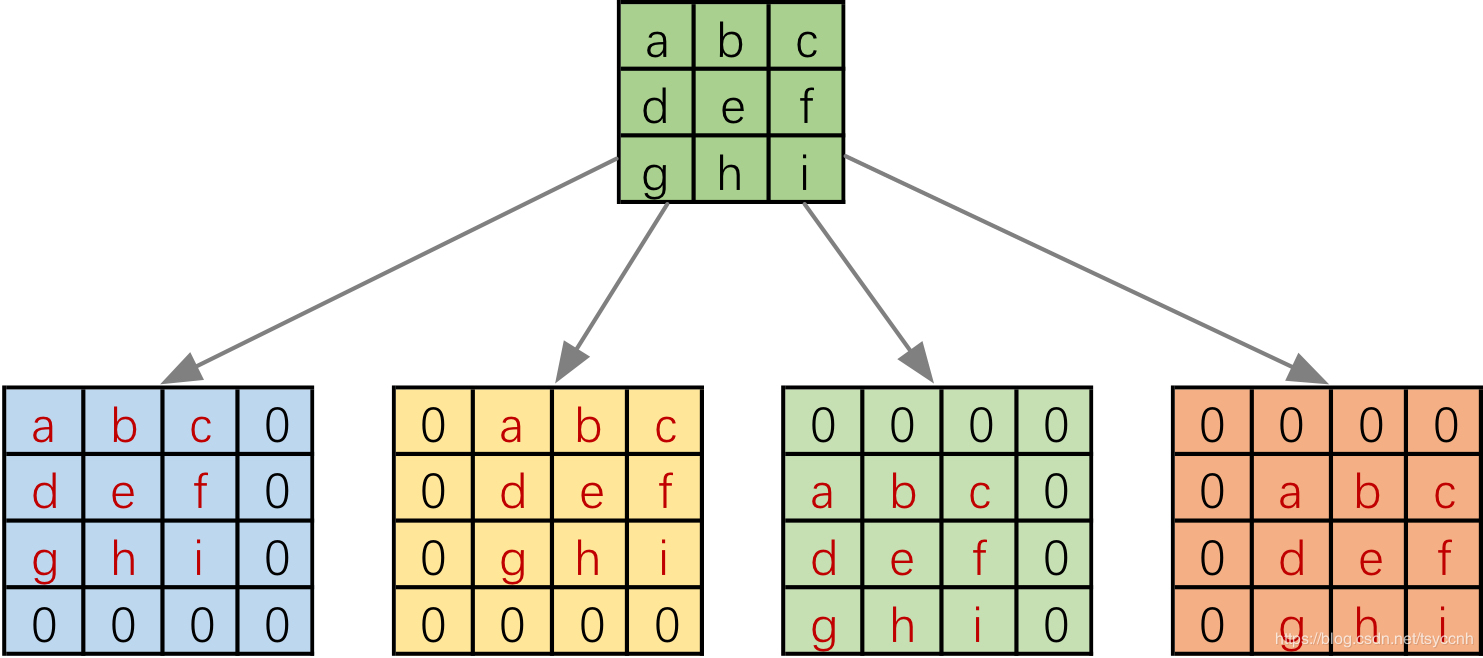
进一步的,我们将输入拉成长向量,四个4x4卷积核也拉成长向量并进行拼接,如下图。
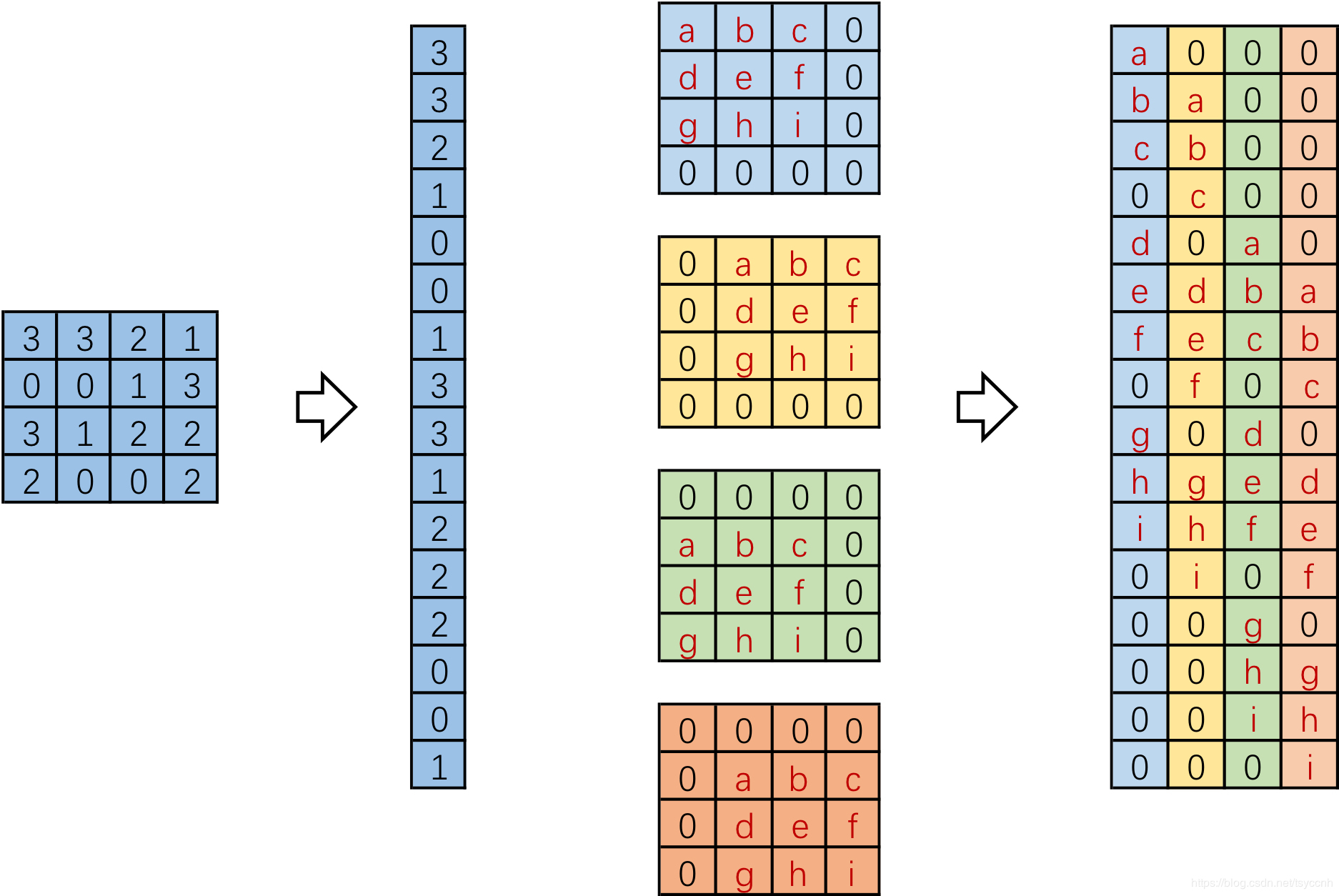
我们记向量化的图像为 I,向量化的卷积矩阵为 C,输出特征向量为 O

如下图所示。
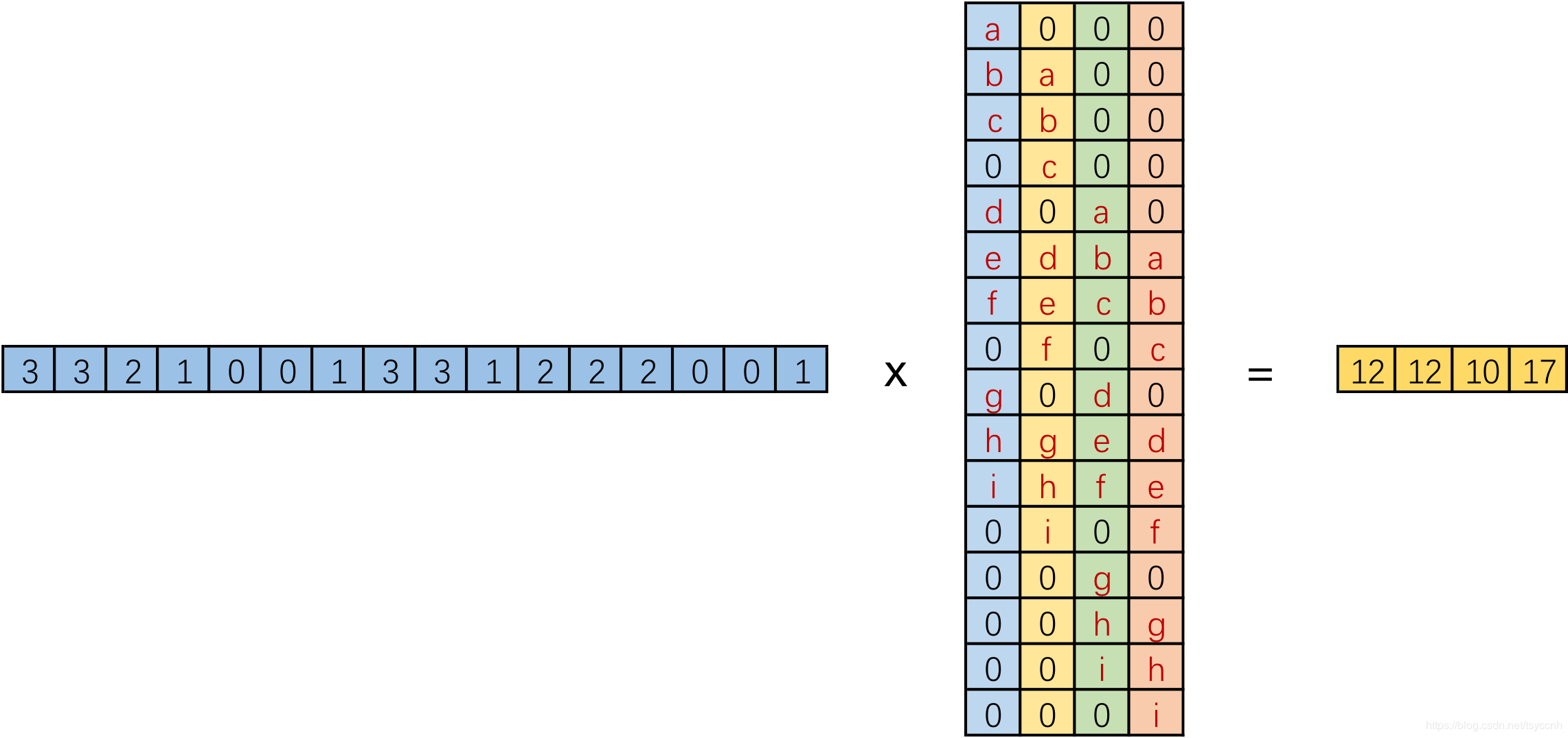
我们将一个1x16的行向量乘以16x4的矩阵,得到了1x4的行向量。那么反过来将一个1x4的向量乘以一个4x16的矩阵是不是就能得到一个1x16的行向量呢? 没错,这便是转置卷积的思想。
转置卷积
一般的卷积操作(我们这里只考虑最简单的无padding, stride=1的情况),都将输入的数据越卷越小。根据卷积核大小的不同,和步长的不同,输出的尺寸变化也很大。但是有的时候我们需要输入一个小的特征,输出更大尺寸的特征该怎么办呢?比如图像语义分割中往往要求最终输出的特征尺寸和原始输入尺寸相同,但在网络卷积核池化的过程中特征图的尺寸却逐渐变小。在这里转置卷积便能派上了用场。在数学上,转置卷积的操作也非常简单,把正常卷积的操作反过来即可。
对应上面公式,我们有转置卷积的公式:
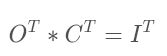
如下图所示:

这里需要注意的是这两个操作并不是可逆的,对于同一个卷积核,经过转置卷积操作之后并不能恢复到原始的数值,保留的只有原始的形状。
所以转置卷积的名字就由此而来,而并不是“反卷积”或者是“逆卷积”,不好的名称容易给人以误解。
形象化的转置卷积
但是仅仅按照矩阵转置形式来理解转置卷积似乎有些抽象,不像直接卷积那样理解的直观。所以我们也来尝试一下可视化转置卷积。前面说了在将直接卷积向量化的时候是将卷积核补零然后拉成列向量,现在我们有了一个新的转置卷积矩阵,可以将这个过程反过来,把16个列向量再转换成卷积核。以第一列向量为例,如下图:

这里将输入还原为一个2x2的张量,新的卷积核由于只有左上角有非零值直接简化为右侧的形式。对每一个列向量都做这样的变换可以得到:
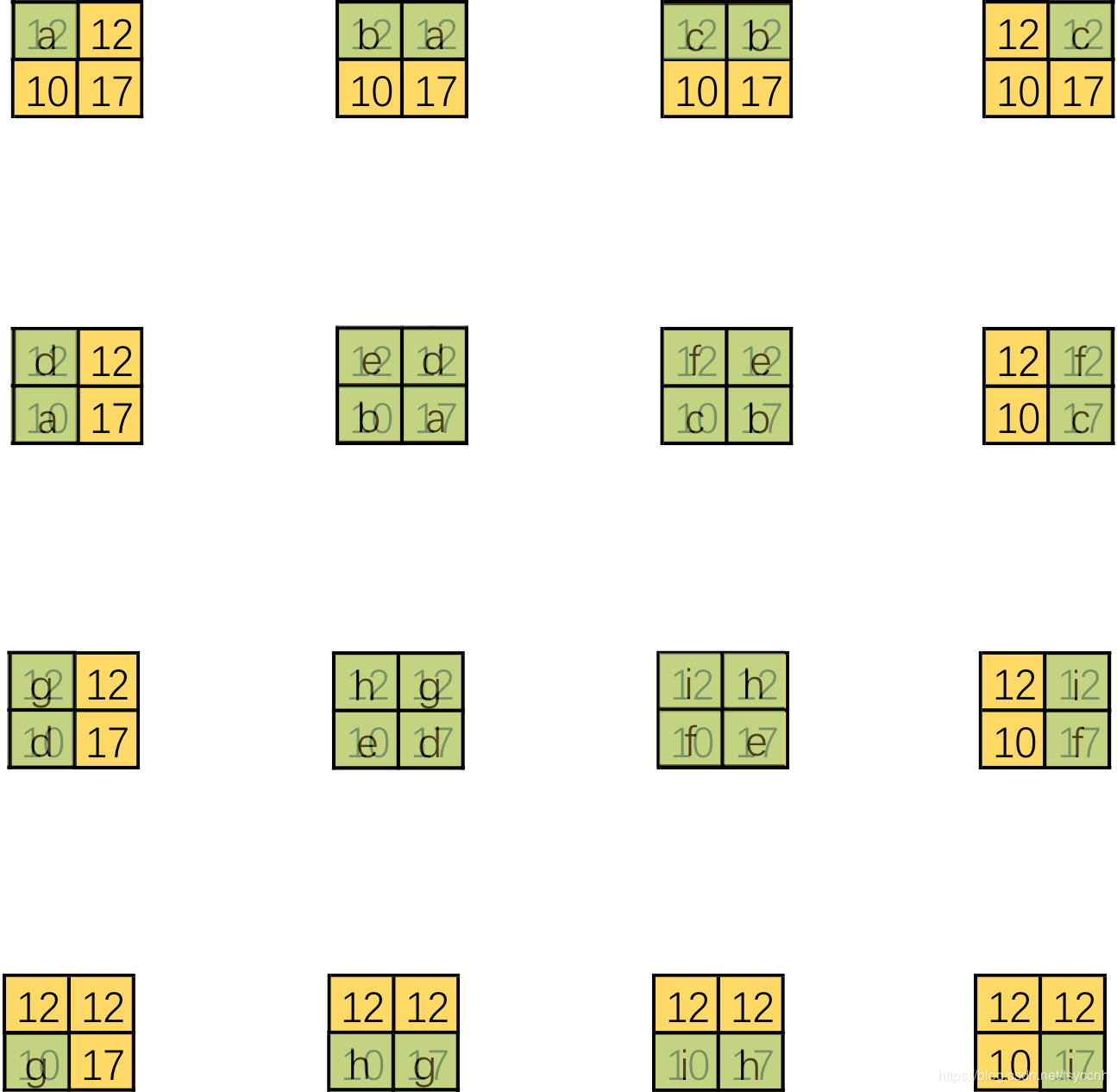
这是一个很有趣的结果,结合整体来看,仿佛有一个更大的卷积核在2x2大小的输入滑动。但是输入太小,每一次卷积只能对应卷积核的一部分。我们来把更大的卷积核补全,如下图:
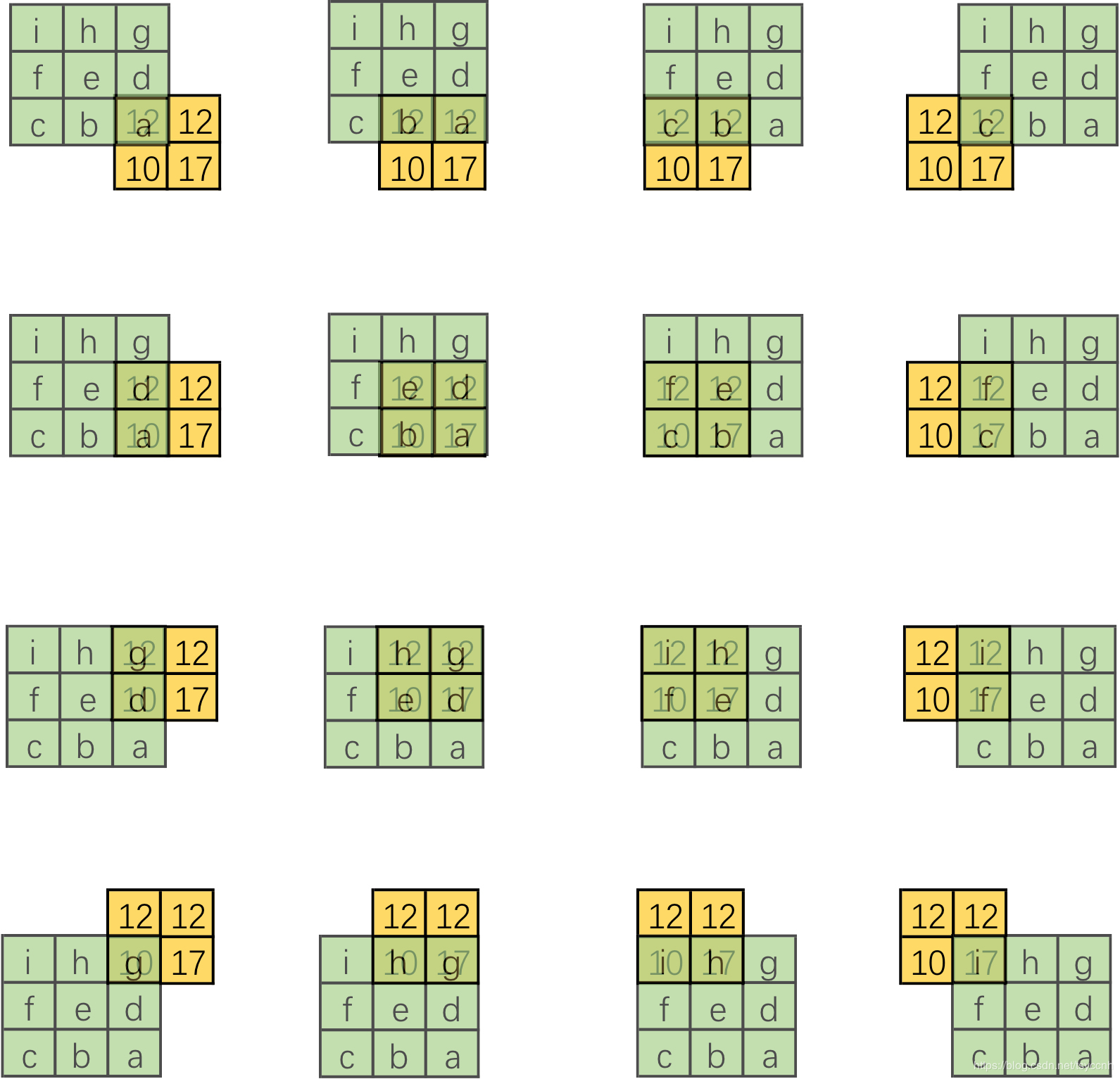
这里和直接卷积有很大的区别,直接卷积我们是用一个“小窗户”去看一个“大世界”,而转置卷积是用一个“大窗户”的一部分去看“小世界”。这里有一点需要注意,我们定义的卷积核是左上角为a,右下角为i,但在可视化转置卷积中,需要将卷积核旋转180°后再进行卷积。由于输入图像太小,我们按照卷积核尺寸来进行补零操作,每边的补零数量显而易见是2,即3-1。这样我们就将一个转置卷积操作转换为对应的直接卷积。如下图:
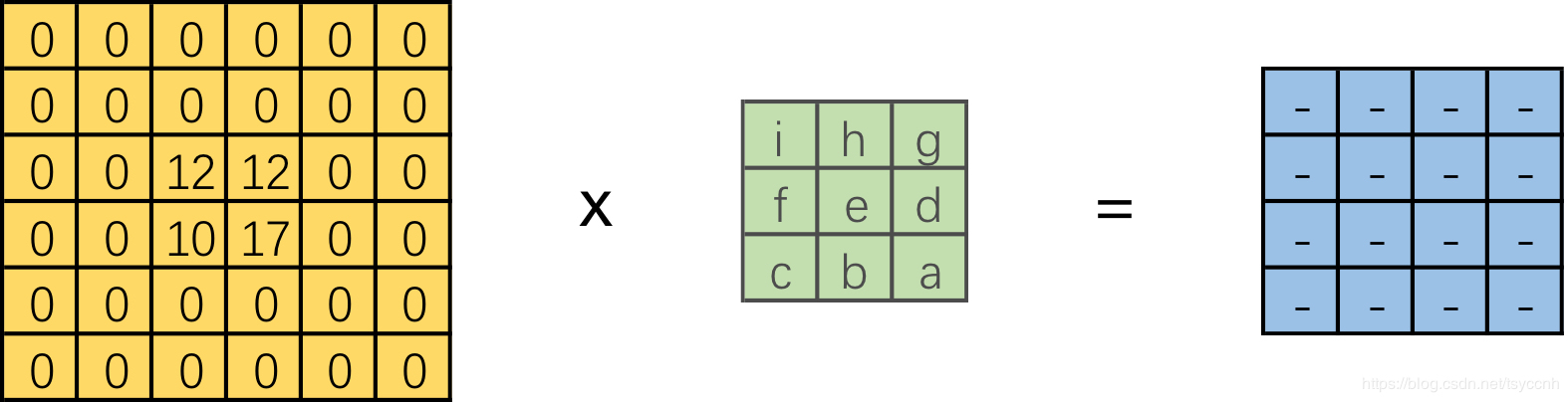
总结一下将转置卷积转换为直接卷积的步骤:(这里只考虑stride=1,padding=0的情况)
设卷积核大小为k*k,输入为方形矩阵
- 对输入进行四边补零,单边补零的数量为k-1
- 将卷积核旋转180°,在新的输入上进行直接卷积
对上面的结论我们在TensorFlow中验证一下。
验证实验代码:
首先调用TensorFlow的conv_transpose函数来进行转置卷积
import tensorflow as tf
x = tf.reshape(tf.constant([[1,2],
[4,5]],dtype=tf.float32), [1, 2, 2, 1])
kernel = tf.reshape(tf.constant([[1,2,3],
[4,5,6],
[7,8,9]],dtype=tf.float32), [3, 3, 1, 1])
transpose_conv = tf.nn.conv2d_transpose(x, kernel, output_shape=[1, 4, 4, 1], strides=[1,1,1,1], padding='VALID')
sess = tf.Session()
print(sess.run(x))
print(sess.run(kernel))
print(sess.run(transpose_conv))
输出结果如下:
tf转置卷积
input: 1 2
4 5
kernel: 1 2 3
4 5 6
7 8 9
output: 1 4 7 6
8 26 38 27
23 62 74 48
28 67 76 45接下来按照上面的方式,将转置卷积转换为一个等效的直接卷积
# 转换为等效普通卷积
x2 = tf.reshape(tf.constant([[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 1, 2, 0, 0],
[0, 0, 4, 5, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0]],dtype=tf.float32), [1, 6, 6, 1])
kernel2 = tf.reshape(tf.constant([[9,8,7],
[6,5,4],
[3,2,1]],dtype=tf.float32), [3, 3, 1, 1])
conv = tf.nn.conv2d(x2,kernel2,strides=[1,1,1,1],padding='VALID')
print(sess.run(x2))
print(sess.run(kernel2))
print(sess.run(conv))
输出结果和转置卷积相同
等效直接卷积
input: 0 0 0 0 0 0
补零 0 0 0 0 0 0
0 0 1 2 0 0
0 0 4 5 0 0
0 0 0 0 0 0
0 0 0 0 0 0
kernel: 9 8 7
旋转180度 6 5 4
3 2 1
output: 1 4 7 6
输出不变 8 26 38 27
23 62 74 48
28 67 76 45实验结果和我们的预测一致。
步长(Stride)不为0的转置卷积(待添加)
总结
通过这一篇文章,仔细的梳理的了转置卷积由来以及其等效的直接卷积形式。希望以后在使用转置卷积的过程中可以做到心中有数,有画面。有关其他不同参数的转置卷积还有很多,比如当stride不为1时怎么办,padding不为0时怎么办。关于这些细节的讨论建议可以去参看参考文献:https://arxiv.org/pdf/1603.07285.pdf 。这里作者做了更加详尽的讨论,这里就不赘述了。
参考
https://arxiv.org/pdf/1603.07285.pdf
https://iksinc.online/tag/transposed-convolution/
https://zhuanlan.zhihu.com/p/48501100
https://blog.csdn.net/silence2015/article/details/78649734
https://blog.csdn.net/u014722627/article/details/60574260
来源:CSDN,作者:史丹利复合田
原文:https://blog.csdn.net/tsyccnh/article/details/87357447
版权声明:本文为博主原创文章,转载请附上博文链接!






