卷积神经网络中的权值更新也是使用误差的反向传播算法。损失函数一般使用最小平方误差函数。由于卷积网络中存在两部分区域:卷积区和全连接区,它们在计算损失时有所不同我们将其分开进行讨论。
1、全连接网络的权值更新
这一部分与经典的人工神经网络不同之处在于多了一个偏置值。我们主要对多出的这个偏置值的更新进行分析即可,其他的权值变化和人工神经网络的方法类似。
对于全连接区的第l层的输出函数为:
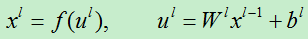
第n个训练样例的误差损失为:

由于在计算输出时有两类参数:权向量w和基值b。现在分别对其计算。我们对其使用梯度下降算法。设网络共有L层
1)对基值b,(其实在每层,b是一个向量)
A)对于第L层损失函数对基的偏导数为:
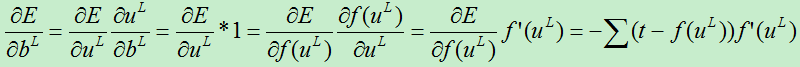
由于每层都有多个特征图,每个特征图都对应一个基值,因为上面的其实求偏导数实际上是对基向量的偏导数。
为了方便表述,我们将误差对基的导数定义为灵敏度,其表达式为:
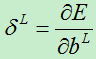
2)对权向量w,(在每层,w是一个矩阵)
A)对于第L层的权值,我们有:
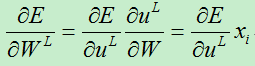

B)对于第l层的权值,求偏导数:

所以权值的改变量为:

2、卷积区的权值更新
由于卷积层和抽样层的计算方式有所不同,我们分别对其进行分析:
1)卷积层误差项分析
由于当前层的权值通过输出作用于下一层的神经元而产生影响,所以在计算误差函数对权值求导时需要使用链接法。首先卷积层的输出为:

由于卷积层的下一层为抽样层,那么首先需要知道在下一层哪些神经元与该卷积层的节点i的联系,然后根据原来的采样方式进行误差分析。由于采样层在从卷积层采样时,同一个结点不会被重复采样,因而,卷积层的一个局部感受野对应采样层中的神经元的一个输入。
假设我们现在分析的卷积层是第l层,则其下一层为l+1层(为池化层)。我们假设第l+1层的误差项为: ,则第l层的节点j的误差项为:
,则第l层的节点j的误差项为:

上式并未考虑到第l层到下一层的权值:
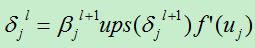
注:为了简便,本人对所有的矩阵,向量运算进行了简化,只把它看成一个单一变量来处理。
其中:Ups (x):对x进行上采样,此处表示下一层的误差项中x的贡献值。
其具体操作要根据前面的pooling的方法,因为下一层的pooling层的每个节点由l层的多个节点共同计算得出,pooling层每个节点的误差敏感值也是由卷积层中多个节点的误差敏感值共同产生的。
A)若前面使用mean-pooling方法,则将下一层的误差项除以下一层所用的滤波器的大小。假如下一层的滤波器的大小为k*k,则:
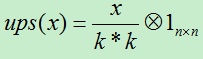
B)若前面使用max-pooling方法,则将需要记录前向传播过程中pooling区域中最大值的位置,然后判断当前的结点是否在最大位置上,若在最大位置上则直接将当前的下一层的误差值赋值过来即可,否则其值赋0。
有了上面了误差损失项,现在我们开始计算损失函数对基的偏导数和对权向量的偏导数:
A)基的偏导数
损失函数对基的偏导数为:
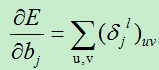
B)权值的变化量
损失函数对权值的偏导数为:
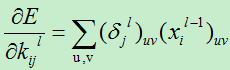
2)池化层(抽样层)误差项分析
对于采样层,其输出值计算公式为:

其中down(xj)为神经元j的下采样。
在这里我们向上面卷积层一样,需要先计算出误差项,然后通过误差项就可以计算得到其他权值和偏置。
由于采样层的下一层为卷积层,采样层的每个节点可能被卷积多次。假如当前的采样层为第l层,我们需要计算第j个结点的神经元的误差,则我们首先需要找到第l+1层中哪些神经元用到过结点j,这需要我们在将l层卷积到l+1层的时候保存神经元的映射过程,因为在计算反向传播误差时需要用到。先假设第l+1层中用到结点j的神经元的集合个数为M,
则第l层的误差项为:
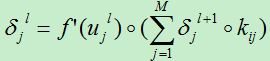
现在我们可以很轻松的对训练偏置和位移偏置的导数:
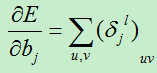
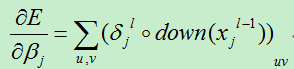
总结
上面的关于卷积区的权值的更新需要用到矩阵,向量的内积等操作,在文中大部分地方故意将此进行了弱化,以便于表达式的精简。
其实在上面误差的分析过程中,最核心的步骤就是求解误差项(又称灵敏度),其他的计算都是以此为基础。误差项的求解首先要分析需要计算的结点j与下一层的哪个或哪些节点节点有关联,因为结点j是通过下一层与该节点相连的神经元来影响最终的输出结果,这也就需要保存每一层节点与上一层节点之间的联系,以便在反向计算误差时方便使用。
总之,卷积神经网络的误差分析其核心思想与人工神经网络类似,都是通过反向逐层影响的方法来分析误差。
本文转自:博客园 - liuwu265,转载此文目的在于传递更多信息,版权归原作者所有。