作者: 张建中
统计计算概述
统计计算(Statistical Computing),又称概率统计计算、计算统计或计算机统计,是概率论、数理统计和应用统计、数学和计算机科学等学科之间的交叉性、边缘性、融合性和应用性的计算数学的一个分支,数学技术中的一类常用算法。
统计计算早已有之,和概率统计有着同样长的发展史,只是由于计算机的出现和网络技术的发展,解决了巨量计算、海量数据采集、存贮和传输等困难,才得到了较快发展和大量应用。统计计算软件的发展和普及,同计算机图形、图表及数据库等数学技术的有机结合,计算机网络的发展使全球数据得以共享,进一步推动了统计计算的快速发展和广泛应用。
统计计算,研究如何根据实际问题提出的要求,利用概率统计中提供的数学模型,计算数学中提供的有效算法及其自身发展起来的一些特别有效的算法,对数据进行统计分析,挖掘其中隐含的信息和知识,对问题做出科学的分析、合理的分类、可用的预测和辅助性决策,给出实际问题的统计描述和统计控制等结果。因此,现在组成了大数据处理中很重要的一类算法。
统计计算是处理海量数据的科学,是用海量计算替代理论公式推导的一组工具,开辟了统计理论和算法研究的一条新途径、一类新方法。
统计计算研究的主要范围包括海量数据的处理和分析,如数据预处理、数据分析计算、数据挖掘计算、多元统计分析计算、时序分析计算,随机模型模拟的蒙特卡罗方法,在计算机上实现具体计算的软件等多个相互关联的方面。同时,利用计算机高速实现数值运算和逻辑运算的特点,推出了一系列和传统统计计算不同的算法,如各种探索性数据分析算法、非参数统计算法、稳健性统计算法,神经元网络算法,遗传性搜索算法和再抽样算法等等,大大丰富和增强了统计计算处理实际问题的能力。现对其所含内容简介如下。
随机数据的统计分析计算
在计算机上,对实际问题中给出的一组试验观测数据或概率统计模型的随机模拟数据x1,x2 ,…,xn 进行分析计算。这里,xi=(xi1,xi2,…,xim),(i=1,2,…,n;m≧1) 表示在第i次试验中或第i次模拟中得到的观测数据,可以是一个标量 (m=1),也可以是一个向量(m>1)。根据xi所含变量个数m的不同(m=1或m>1)和各次观测模拟之间是否统计相关或相互独立,在分析计算时使用不同的概率统计模型和不同的概率统计算法。对各次观测或模拟间相互独立的随机数据,有一元(m=1)和多元(m>1)统计分析计算之分;对相关性的观测数据,有处理平稳随机数据的数字时间序列分析计算,处理突发随机事件的随机点过程计算,处理状态离散的马尔可夫链计算和处理各种观测系统的数字滤波计算等。
对一组给定的随机观测数据{xi}进行统计分析计算,重要的是选择恰当的概率统计模型和有效的进行统计分析计算的算法。以对多元数据进行统计分析计算为例,目的各有不同:有的要求对观测变量之间进行调整,使它们之间可以进行平衡和便于比较;有的要求在不影响结果的精度和可靠度的条件下,降低观测数据的维数,化简问题的结构;有的要求按照一定的标准,对数据进行分类或分组;有的要求给出观测数据的方程或方程组,用这类模型解释因变量的变异,预测系统的未来可能取值等等。因此,在多元分析计算中,不仅要明确进行分析计算的目的和观测数据{xi}自身的一些性质和特点,而且还要了解各种不同的多元统计分析模型及其相应算法的特点。在多元统计分析计算中,进行统计分析的主要目的、相应可用的统计模型及其常用算法如图所示(箭头指示出可选用的统计模型)。
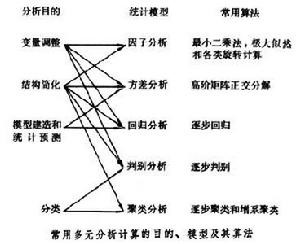
以多元回归分析和多元判别分析为例,用这种统计分析模型进行计算,就是根据由变量组(x1,x2,…,xm;y)得到的相互独立的 n组观测数据(xi1,xi2,…,xim;yi)(i=1,2,…,n;n>m), 确定因变量y和自变量(x1,x2,…,xm) 之间的关系,用于识别、预报、控制或分类。这里,因变量y在回归模型中取连续值,表示分析系统所处的水平;在判别模型中取离散值,表示系统的类别。对这组数据进行统计分析计算的目的,就是从给定的变量组(x1,x2,…,xm)中,选取一个“最优”的子集:在回归模型中,经计算给出回归方程
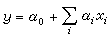
能够解释因变量y的变异;在判别模型中,经计算给出判别函数,能够将用y表示的类别数据按类分开。所以,对给定的观测数据进行分析计算时,主要注意力集中在最优变量子集选取的不同算法及其实现上。在实际问题中,预选自变量的个数m和观测的次数n通常都很大,各个自变量之间也不相互正交,存在着错综复杂的相互关系,需要按照一定的标准对自变量xi进行舍选。目前常用的算法有四种:①渐增法,把自变量按照各自重要性的大小,逐个选入回归方程或判别函数;②渐降法,先把所有能引入的自变量全部引入回归方程或判别函数,然后再把不重要的自变量逐个舍去;③舍选法,在把重要的自变量引入回归方程或判别函数的同时,检验已在模型中的自变量是否继续显著,把不符合要求的自变量从中舍去;④最佳子集法,利用自变量各个不同子集合之间的关系,从所有可能的子集中选取最佳的子集。第三种算法最为常用,通常把它称为逐步回归和逐步判别算法。
对系统中依赖于时间t的一个变量或一组变量x(t)进行观测或模拟,在时间t的等距间隔Δt上,得到一组有序离散相关的数集合x1,x2,…,xn,其中xi=x(t0+iΔt)(i=1,2,…,n)称为数字时间序列,分析这类数据的方法称为数字时间序列分析,或简称为时间序列分析。这类方法包括时域中的相关分析,频域中的谱分析和时间序列模型,特别是p阶自回归、q阶滑动平均线性模型ARMA(p,q)的识别、估计和检验的计算问题等。
时间序列分析与回归分析、判别分析等多元分析方法相比,发展较迟。由于在实际问题中应用的重要性和广泛性,特别是数字计算机的迅速发展和一些重大算法(如快速傅里叶变换算法 FFT)和理论(如模型识别理论)的突破,从一维时间序列到多维时间序列、从线性模型到非线性模型,都有很快的发展和广泛的应用。
概率统计模型的随机模拟计算
随机抽样是概率统计中的一类经典方法。由于数字计算机的出现和发展,随机抽样作为一种算法在第二次世界大战之后得到了迅速发展,并在许多不同的领域中得到了广泛的成功应用。当时从事这一方法研究的物理学家,借用欧洲著名赌城蒙特卡罗(Monte Carlo)的名字,给该法起名为蒙特卡罗法。
和随机数据的统计分析计算不同,随机模拟计算利用实际系统的概率统计模型,通过模拟计算,“仿造”系统的试验观测数据,进而分析系统的渐近统计性质。在数字计算机上,随机模拟计算用系统概型的随机数字模拟代替实际系统的物理模拟,用伪随机数代替随机变量的真实抽样,这种双重模拟计算,为概率统计计算解决实际问题开辟了不少新的应用领域。鉴于蒙特卡罗法的算法上的重要性和应用的普遍性,下面将另外开辟新的一节进行介绍。
概率统计计算程序包
为方便使用者在计算机上使用统计算法已经研制出为数众多的概率统计计算程序包,它们可提供完整配套的统计模型,快速可靠的算法,易于使用、便于移植和二次开发的各种计算机语言的程序。它们在计算机上的广泛应用,既带来了方便,也出现了一些值得注意的问题,主要集中在概率统计计算的误用和滥用上。因此,具有模型自动检验、识别功能和有效算法选取功能的统计程序包更受到使用者的欢迎。
作者: 张建中
出处:http://zhangjianzhong.blog.kepu.cn/20170531091609.html






