近年来深度学习在图像识别、语音识别等领域得到了广泛的应用,取得了优异的效果,但深度学习网络的结构设计没有一般规律可循。本文基于卷积神经网络和递归卷积神经网络模型探究了深度学习网络不同层级间参数分布对网络性能的影响,在CIFAR-10、CIFAR-100和SVHN数据集上进行了大量的实验。结果表明:在保证网络总参数大致相等并稳定在饱和的临界值附近的条件下,增加高层参数数量的能够提升网络性能,而增加低层参数数量的会降低网络性能。通过这一简单的规则,我们设计的递归卷积神经网络模型结构在CIFAR-100和SVHN两个数据集上达到了目前单模型最低的识别错误率。
1. 引言
深度学习自提出以来,在图像识别、目标检测、语音识别等领域取得了突破性的进展。作为深度学习的重要组成部分,卷积神经网络(Convolutional Neural Network,简称 CNN)[1] [2]在各领域中的应用日趋广泛。卷积神经网络采用局部感受野和权值共享的处理方法,比较吻合高级动物的视觉系统结构和功能,广泛地应用于图像识别和检测、语音识别等领域,并取得了优良的效果[3]-[5]。但当前卷积神经网络由低层到高层的神经元和权值数量的分布没有一定的规则,导致同样的网络结构,无法保证获得最优化参数。
大脑皮层不同层级的神经元数量以及层级之间连接的权值数量分布具有一定的规律性。在认知神经科学中认为,大脑的认知过程是分级的。以视觉系统为例,在大脑中,初级视觉皮层(primary visual contex,V1 区)通过外侧膝状体的中继,接受来自眼的视觉信息,V2 区接近 V1 区,并接收来自 V1 区的传入,且具有比 V1 区大得多的感受野。V3 区和 V4 区靠近 V2 区并接收来自 V2 区的传入[6]。通常,信息经过低层神经元转换到高层神经元的过程中,神经元突触的数量被认为是扩张的,离开 V1 区比进入 V1 区,神经突触数量扩张了 25 倍[7]。后来,神经科学家们相继在躯体知觉系统、听觉系统,等认知系统中发现了类似的神经元扩张规律[7]。不同区的突触数量可以对应于人工神经网络中不同层级中的参数数量。因此,神经科学中神经元突触数量分布的这种规律对人工神经网络低层和高层参数数量的设置具有一定的启发性。为了更好的模拟生物大脑从而为卷积神经网络获得更优的参数设置方法,探究神经科学中的这种规律性是否同样适用于卷积神经网络是重要而且必要的。本文依据计算神经科学家们对生物大脑皮层不同层级的神经元数量和层级之间的连接权值数量的实验研究,采用 CNN 模型和基于 CNN 推广的递归卷积神经网络模型(Recurrent Convolutional Neural Network,简称 RCNN),在 CIFAR-10、CIFAR-100 和SVHN 数据集上进行了实验结果分析,总结出在卷积神经网络中不同层神经元数量的分布对网络性能的影响,提出一条简单有效的提高网络性能的方法。
2. 卷积神经网络与递归卷积神经网络
2.1. 卷积神经网络
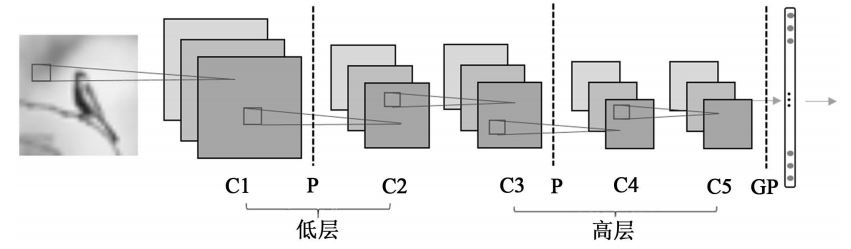
卷积神经网络的主要操作为卷积(Convolution)和降采样(Pooling),实际上是一种网络自动提取特征的过程。经过卷积和降采样操作,扩大了人工神经元的感受野范围,使得层次越高的神经元获得更多的全局信息。本文采用具有五层卷积操作的网络结构,如图 1 所示,其中卷积操作均采用步长为 1,偏置为 2的卷积方式,使得卷积前后特征图大小不变,第一层卷积层卷积核大小为 5 × 5,其他各卷积层卷积核大小均为 3 × 3。在第一层卷积层和第三层卷积层后进行最大化降采样(Max Pooling),降采样范围均为 3 × 3,步长为 2 。第五层卷积层后进行全局降采样(GlobalMax Pooling,以下简称 GP),得到 1 × 1 的输出。在每个卷积层之后进行非线性操作,激活函数均为 ReLu 函数 f x x = max 0, ( ) ,降采样之后均进行局部归一化操作(Local Response Normalization,简称 LRN),最后经过一层全连接层输出给 softmax 分类器进行分类。
2.2. 递归卷积神经网络
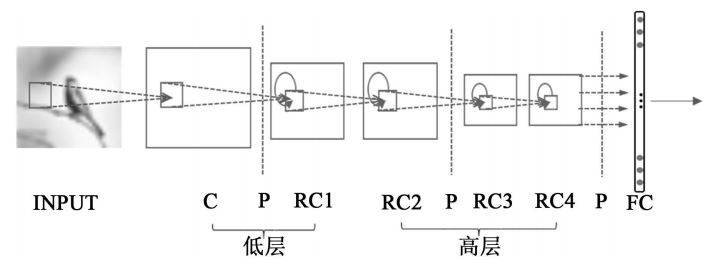
递归卷积神经网络是卷积神经网络的一种推广[8]。在神经科学中已经证明生物视觉系统中神经元之间存在大量的递归连接[9],从而可以充分的利用上下文信息。在传统的卷积神经网络中,只有高层神经元获得了较多的全局信息,而低层神经元只能获得一定范围内的局部信息。为了弥补这一缺陷,递归卷积神经网络在传统卷积神经网络的基础上引入了卷积层内的递归连接构成递归卷积层(Recurrent-Convolutional,RC 层,见图 2),
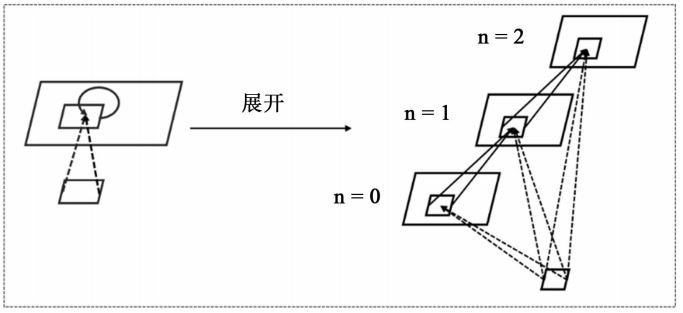
递归卷积层为递归卷积神经网络的核心部分,每个递归卷积层内进行权值共享,可以将其按时间迭代展开,如图 3 所示。在传统卷积神经网络中,对于第 n 层卷积层第 k 个特征图上 (i , j ) 位置的神经元,其接收到的输入为:

其中 wn,k 为该特征图上对于位置的神经元权值矩阵,un,k,( i , j ) 为该神经元覆盖的特征图输入矩阵,bk 为偏置矩阵。而在递归卷积层中,神经元除了接收前一层传递而来的前馈输入,还接收自身卷积递归迭代所得信息。即当迭代次数为 n 时,对于位于递归卷积层中第 k 个特征图 ( i , j ) 位置的神经元所接受到的输入zk,( i , j ) 为:
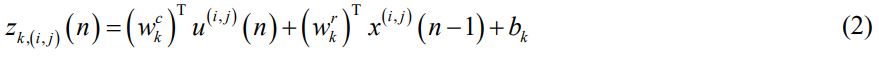
其中 u( i , j )( n ) 为神经元所接收到的前馈输入,即公式(1),x( i , j ) ( n − 1 ) 为神经元所接收到的递归输入,wkc 和 wkr 分布为前馈神经元和递归神经元权值矩阵,bk 为偏置矩阵。每次迭代使得神经元感受野扩大,使得即使在低层的所有神经元同样可以得到高层信号的调制作用,从而获得更加全局化的信息。实验证明,这种调制信号所带来的上下文信息对于卷积神经网络处理机器视觉任务,如目标识别[8]和图像分割[10]等,具有重要的作用。本文采用与[8]文中相同的网络结构,如图 2 所示。图像输入经过一层卷积层之后进行降采样,所得信息依次传入第一层递归卷积层、第二层递归卷积层,经过第二次降采样之后传入第三层递归卷积层、第四层递归卷积层,每个递归卷积层中递归卷积迭代 3 次,再经全局降采样(Global Max Pooling)之后直接输入给 softmax 分类器。卷积层和递归卷积层前馈输入均进行非线性(ReLu)和局部归一化(LRN)操作。
3. 实验数据集
实验数据采用 CIFAR-10、CIFAR-100 和 SVHN 数据集。CIFAR-10 数据集包含飞机、汽车、鸟、猫等 10 类物体,每类包括 5000 张训练图片和 1000 张测试图片,即共有 5 万张训练图片和 1 万张测试图片,图片大小为 32 × 32。CIFAR-100 数据集与 CIFAR-10 数据集类似,包含常见的 100 类物体,例如苹果、汽车、船等,每个类别包括 500 张训练图片和 100 张测试图片,共计 5 万张训练图片和 1 万张测试图片。SVHN 数据集(The Street View House Numbers Dataset)是从谷歌街景图片中取出的门牌号图片,实验中采用官网提供的第二种数据格式。SVHN数据集共包含630,420张图片,10类数字,图片大小同样为32 × 32,分为训练集、测试集和拓展数据三个部分,其中训练集包括 73,257 张图片,测试集包括 26,032 张图片,剩余为拓展数据集。在实验中采用与[11]相同的验证集,即从训练集中每类随机抽取 400 张并从拓展数据集中每类随机抽取 200 张作为验证集。
所有数据均进行减均值预处理,即对数据集每张图片的 R、G、B 通道减去数据集所有图片该通道的均值。所有实验结果均在未作数据扩展(dataaugmentation)的条件下所得,实验基于 cuda-convnet2 [12]深度学习框架,运用两块 Titan Blackx GPU 加速实现。
4. 实验设计与结果分析
由于两个模型在全连接层前均进行了全局降采样,全连接层参数相对于网络总参数可忽略不计,只考虑卷积层或递归卷积层的参数。对于卷积神经网络模型和递归卷积神经网络模型,均设计 A、B 两组变种,每组包括基准模型(A2,B2)、在基准模型的基础上增加低层参数数量的模型(A1,B1)和在基准模型的基础上增加高层参数数量的模型(A-3,B-3),并尽量保证 A、B 两组组内模型总参数一致。由于cuda-convnet2 要求每层的特征图个数必须为 32 的倍数,所以难以要求同组内各模型的总参数数量精确相同。每个基准模型各层的特征图数目 N 均相同,但 A2 和 B2 的 N 不相同,导致它们的总参数数量不相同。为减化讨论,对于卷积神经网络,我们设定第一、第二个卷积层为低层卷积层,第三、四、五个卷积层为高层卷积层(见图 1);对于递归卷积神经网络,设定卷积层与第一个递归卷积层为低层,第二至第四个递归卷积层为高层(见图 2)。
4.1. CIFAR-10
对于卷积神经网络的基准模型 CNN-A2 各层的特征图数设为 160,CNN-B2 各层的特征图数设为 192,两个基准模型的总参数分别为 0.95M 和 1.34M,实验结果见表 1。由测试结果可以看出,更多的参数并没有给 CNN 带来更好的实验结果,即 CNN-B2 相对于 CNN-A2 发生了过拟合。
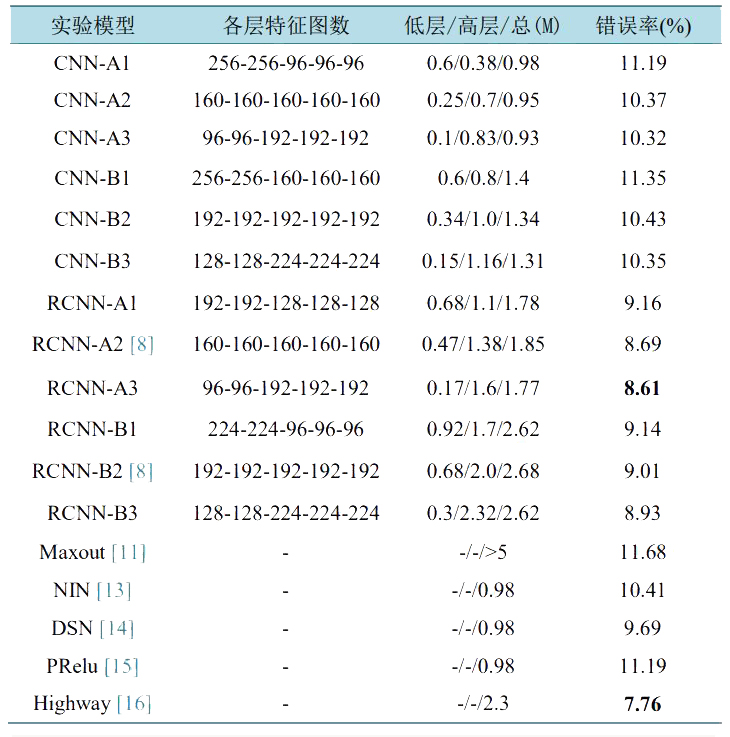
在基准模型 CNN-A2 的基础上增加低层参数数量并降低高层参数数量,测试错误率由 10.37%增加到11.19%;而增加高层参数量并减少低层参数量,错误率降低到 10.32%。在基准模型 CNN-B2 的基础上增加低层参数数量同时减少高层参数数量,错误率从 10.43%升高到 11.35%;而增加高层参数数量同时减少低层参数数量,错误率降为 10.35%。实验结果表明:在 CIFAR-10 的卷积神经网络模型实验中,在总的参数数量不变的情况下,增加网络高层参数可以提高网络测试准确率;增加网络低层参数使得网络测试准确率降低。
参考卷积神经网络的基准模型,递归卷积神经网络的基准模型 RCNN-A2 各层的特征图数设为 160,RCNN-B2 各层的特征图数设为 192。通过分别增加和减少高层和低层的特征图数,进行训练测试,我们得出了与卷积神经网络实验中相同的结论(见表 1)。同时,RCNN-A3 得到相当具有竞争力的测试结果,测试错误率为 8.61%,仅高于尚未正式发表的文献[16]中的结果。
4.2. CIFAR-100
对于 CIFAR-100 数据集,采用与 CIFAR-10 相同的实验设计。即对于卷积神经网络模型和递归卷积神经网络模型,基准模型 A2 各层的特征图数设为 160,基准模型 B2 各层特征图数设为 192,实验结果见表 2。对于基准模型 CNN-A2,网络总参数为 0.96 M,在此基础上,模型 CNN-A1 减少高层参数数量至 0.6M,并增加低层参数数量至 0.38M,总参数数量与基准模型 CNN-A2 保持一致,实验测试错误率由34.06%增加到 37.64%;模型 CNN-A3 减少低层参数数量至 0.1 M 并增加高层参数数量至 0.85 M,总参数数量不变,实验测试错误率降低至 33.79%。基准模型 CNN-B2 网络总参数为 1.34 M,测试错误率为 33.47%,增加低层参数数量同时减少高层参数数量得到模型 CNN-B1 的实验测试错误率为 36.32%;
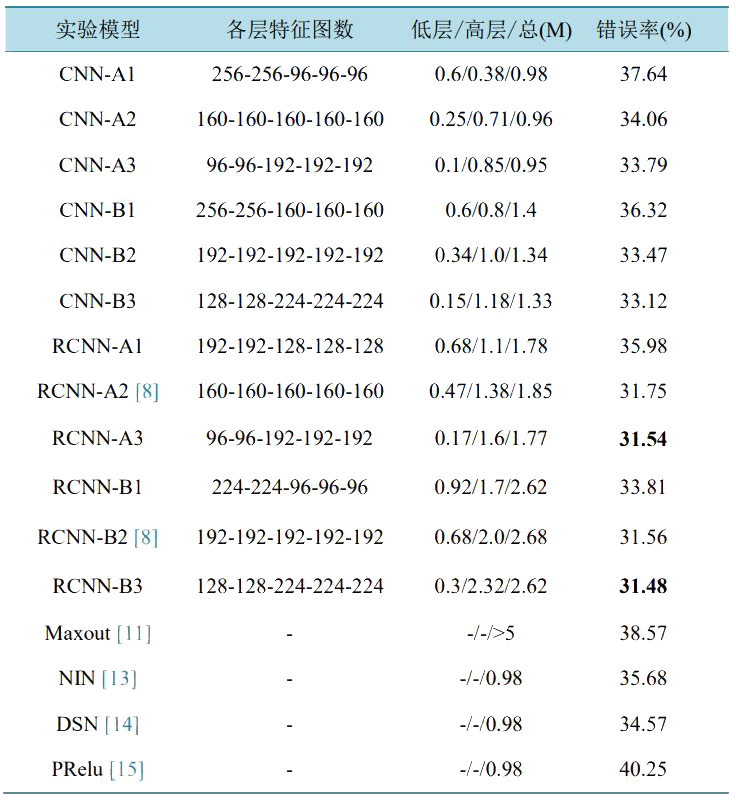
增加高层参数数量并减少低层参数数量,得到模型 CNN-B3 实验测试错误率为 33.12%。同样的,在递归卷积神经网络模型实验中,模型 RCNN-A1 在基准模型 RCNN-A2 的基础上增加低层参数数量并减少高层参数数量,实验测试错误率由基准模型 RCNN-A2 的 31.75%增加至 35.98%;而模型 RCNN-A3 增加高层参数数量减少低层参数数量,实验测试错误率下降为 31.54%。基准模型 RCNN-B2 测试错误率为 31.56%,将基准模型低层参数数量增大、高层参数数量减小的模型 RCNN-B1 测试错误率增大至 33.81%;而将基准模型高层参数数量增大、低层参数数量减小的模型 RCNN-B3,测试错误率减小为 31.48%。
由此可得,在 CIFAR-100 数据集上,同样存在模型总参数不变的情况下,增加高层参数数量有益于提高模型的性能,而增加低层参数数量,反而会使得网络性能降低。另一方面,模型 RCNN-A3 和模型RCNN-B3 在与[8]文中具有相同参数的基准模型 RCNN-A2 和基准模型 RCNN-B2 相比,取得了优良的结果。
4.3. SVHN
对于 SVHN 数据集,同 CIFAR-10 和 CIFAR-100,CNN 基准模型 CNN-A2 各层特征图数为 160,基准模型 CNN-B 各层特征图数为 192;RCNN 基准模型 RCNN-A2 各层特征图数为 160,基准模型 RCNN-B2 各层特征图数为 192,实验结果见表 3。
基准模型 CNN-A2 总参数为 0.95M,错误率为 2.87%,在基准模型基础上增加低层参数并降低高层参数得到模型 CNN-A1 测试错误率为 2.91%;增加高层参数并降低低层参数得到高层模型 CNN-A3 错误率为 2.81%。基准模型 CNN-B2 总参数为 1.34M,错误率为 2.82%,在此基础上,增加低层参数并降低高层参数得到模型 CNN-B1 错误率为 2.89%;增加高层参数并降低低层参数得到模型 CNN-B3 错误率为2.76%。基准模型 RCNN-A2 总参数为 1.85M,错误率为 1.80%,增加低层参数数量的并减少高层参数数量得到模型 RCNN-A1 错误率为 1.86%;
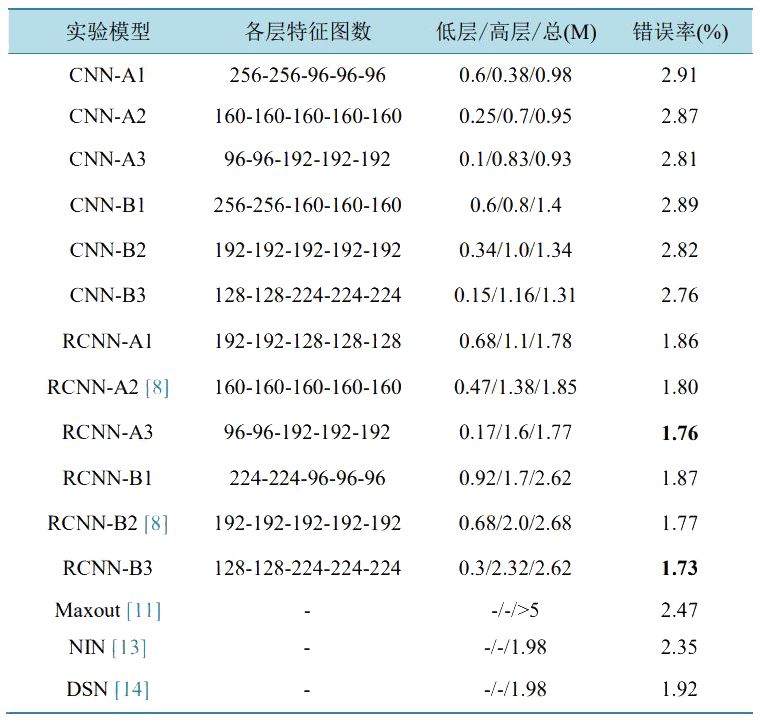
增加高层参数数量的高层并减少低层参数数量得到模型RCNN-A3 错误率为 1.76%;基准模型 RCNN-B2 总参数为 2.68M,错误率为 1.77%,以此为基准,增加低层参数数量减少高层参数数量得到模型 RCNN-B1 错误率增加为 1.87%;而增加高层参数数量减少低层参数数量得到模型 RCNN-B3 错误率降低为 1.73%。可以看出,对于 SVHN 数据集,采用上述 CIFAR-10 和 CIFAR-100 所得到的简单规律,即保证总参数数量基本不变,减少低层参数数量并增加高层参数数量,模型 RCNN-A3 和 RCNN-B3 在取得优秀的测试结果,进一步验证了上述规律。
5. 结论
本文以卷积神经网络和递归卷积神经网络为基础,在 CIFAR-10、CIFAR-100 和 SVHN 数据集上进行了实验研究,探究了在参数数量一定,卷积神经网络和递归卷积神经网络低层参数数量和高层参数数量的变化对网络性能的影响,得到以下结论:网络低层参数数量和网络高层参数数量的分布情况很大程度上影响网络的整体性能。当网络参数数量增加到某一临界值时,在保证此时参数数量不变的情况下减少低层网络参数并增加高层参数数量,可以使得网络性能进一步提升;而当此时增加网络低层参数数量并减少高层参数数量会使得网络性能降低。基于此规律,本文设计的部分模型取得了良好的测试结果,并在 CIFAR-100 和 SVHN 数据集上取得了目前单模型能达到最好的测试准确率。表明这一规律对如何简便有效的提高有监督的深度学习模型的性能具有重要的意义。
基金项目
国家自然科学基金项目(61273023,91420201,61332007)。
参考文献 (References)
[1] Lecun, Y., Boser, B.E., Denker, J.S., et al. (1989) Backpropagation Applied to Handwritten Zip Code Recognition.
Neural Computation, 1, 541-551. http://dx.doi.org/10.1162/neco.1989.1.4.541
[2] Lecun, Y., Boser, B.E., Denker, J.S., et al. (1990) Handwritten Digit Recognition with a Back-Propagation Network.
Advances in Neural Information Processing Systems, 396-404.
[3] Krizhevsky, A., Sutskever, I. and Hinton, G.E. (2012) ImageNet Classification with Deep Convolutional Neural Networks.
Advances in Neural Information Processing Systems, 25.
[4] Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., Erhan, D., Vanhoucke, V. and Rabinovich, A.
(2014) Going Deeper with Convolutions.
[5] Chatfield, K., Simonyan, K., Vedaldi, A., et al. (2014) Return of the Devil in the Details: Delving Deep into Convolutional Nets.
[6] 葛詹尼加, 等, 著. 周晓林, 高国定, 等, 译. 认知神经科学: 关于心智的生物学[M]. 北京: 中国轻工业出版社,2011: 141-177.
[7] Babadi, B. and Sompolinsky, H. (2014) Sparseness and Expansion in Sensory Representations. Neuron, 83, 1213-1226.
http://dx.doi.org/10.1016/j.neuron.2014.07.035
[8] Liang, M. and Hu, X. (2015) Recurrent Convolutional Neural Network for Object Recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.
[9] Dayan, P. and Abbott, L.F. (2001) Theoretical Neuroscience. MIT Press, Cambridge.
[10] Liang, M., Hu, X. and Zhang, B. (2015) Convolutional Neural Networks with Intra-Layer Recurrent Connections for Scene Labeling. Advances in Neural Information Processing (NIPS), 7-12 December 2015, Montréal.
[11] Goodfellow, I.J., Warde-Farley, D., Mirza, M., Courville, A.C. and Bengio, Y. (2013) Maxout Networks. Proceedings of the 30th International Conference on Machine Learning (ICML), 1319-1327.
[12] Krizhevsky, A., Sutskever, I. and Hinton, G.E. (2012) Imagenet Classification with Deep Convolutional Neural Networks.
Advances in Neural Information Processing Systems (NIPS), 1097-1105.
[13] Lin, M., Chen, Q. and Yan, S. (2014) Network in Network. International Conference on Learning Representations (ICLR).
[14] Lee, C.Y., Xie, S., Gallagher, P., Zhang, Z. and Tu, Z. (2014) Deeply Supervised Nets. Advances in Neural Information Processing Systems (NIPS), Deep Learning and Representation Learning Workshop.
[15] Xu, B., et al. (2015) Empirical Evaluation of Rectified Activations in Convolutional Network.
[16] Greff, S.K. and Schmidhuber, J. (2015) Highway Networks. Advances in Neural Information Processing (NIPS),Montréal, 7-12 December 2015.
来源:http://image.hanspub.org:8080/pdf/CSA20151200000_79830787.pdf
文章引用:岳喜斌(北京林业大学工学院,北京), 胡晓林(清华大学计算机科学与技术系,清华信息科学与技术国家实验室,北京), 唐亮
深度学习模型各层参数数目对于性能的影响[J].
计算机科学与应用, 2015, 5(12):445-453. http://dx.doi.org/10.12677/csa.2015.512056






