激活函数的意义(需要激活函数的理由)
激活函数是神经网络的一个重要组成部分。如果不用激活函数(即相当于激活函数为f(x)=x),在这种情况下,网络的每一层的输入都是上一层的线性输出,因此,无论该神经网络有多少层,最终的输出都是输入的线性组合,与没有隐藏层的效果相当,这种情况就是最原始的感知机。
正因为上面的原因,才需要引入非线性函数作为激活函数,这样深层神经网络才有意义,输出不再是输入的线性组合,就可以逼近任意函数。
各类激活函数的优缺点
绝大多数神经网络借助某种形式的梯度下降进行优化,激活函数需要是可微分(或者至少是几乎完全可微分的)。此外,复杂的激活函数也许产生一些梯度消失或爆炸的问题。因此,神经网络倾向于部署若干个特定的激活函数。
Identity
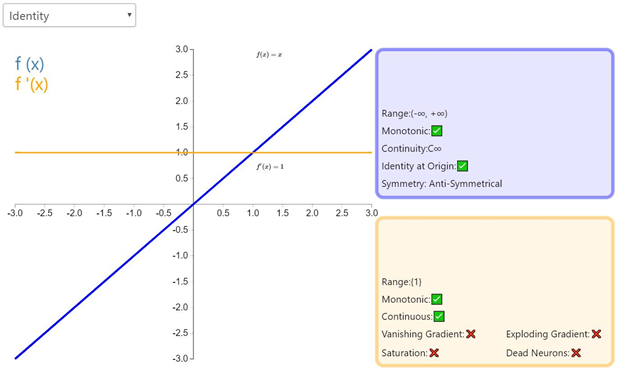
通过激活函数 Identity,节点的输入等于输出。它完美适合于潜在行为是线性(与线性回归相似)的任务。当存在非线性,单独使用该激活函数是不够的,但它依然可以在最终输出节点上作为激活函数用于回归任务。
Sigmoid函数
Sigmoid函数,也就是logistic函数,对于任意输入,它的输出范围都是(0,1)。公式如下:
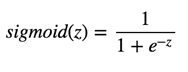
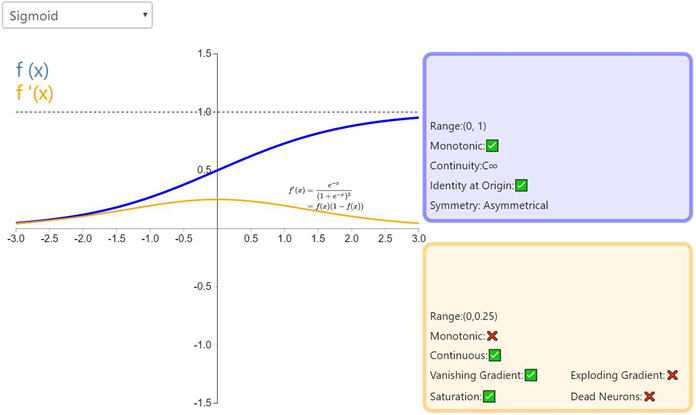
Sigmoid的函数图如上所示,很像平滑版的阶跃函数。但是,sigmoid 有很多好处,例如:
1. 它是非线性的
2. 不同于二值化输出,sigmoid 可以输入 0 到 1 之间的任意值。对,跟你猜的一样,这可以用来表示概率值。
3. 与 2 相关,sigmoid 的输出值在一个范围内,这意味着它不会输出无穷大的数。
但是,sigmoid 激活函数并不完美:
梯度消失。如前面的图片所示,当输入值 z 趋近负无穷时,sigmoid 函数的输出几乎为 0 . 相反,当输入 z 趋近正无穷时,输出值几乎为 1 . 那么这意味着什么?
在这两个极端情况下,对应的梯度很小,甚至消失了。梯度消失在深度学习中是一个十分重要的问题,我们在深度网络中加了很多层这样的非线性激活函数,这样的话,即使第一层的参数有很大的变化,也不会对输出有太大的影响。换句话讲,就是网络不再学习了,通常训练模型的过程会变得越来越慢,尤其是使用梯度下降算法时。
sigmoid 的另一个弊端就是实际运用中指数运算开销太大。尽管有人说,与矩阵乘法或卷积相比,激活函数在深度网络的计算是非常小的一部分,所以这可能不会成为一个大问题。不过,我认为这值得一提。
Tanh函数
Tanh 或双曲正切是另一个深度神经网络中常用的激活函数。类似于 sigmoid 函数,它也将输入转化到良好的输出范围内。具体点说就是对于任意输入,tanh 将会产生一个介于 -1 与 1 之间的值。
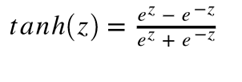
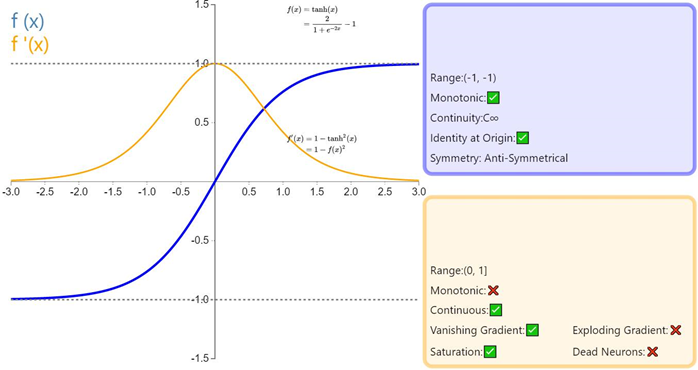
如前面提及的,tanh 激活函数有点像 sigmoid 函数。非线性且输出在某一范围,此处为 (-1, 1)。不必意外,它也有跟 sigmoid 一样的缺点。从数学表达式就可以看出来,它也有梯度消失的问题,以及也需要进行开销巨大的指数运算。
ReLU
终于讲到了 Relu,人们起初并不觉得它的效果会好过 sigmoid 和 tanh。但是,实战中它确实做到了。事实上,cs231n 课程甚至指出,应该默认使用 Relu 函数。
ReLU 从数学表达式来看,运算十分高效。对于某一输入,当它小于 0 时,输出为 0,否则不变。下面是 ReLU 的函数表达式。Relu(z) = max(0,z)
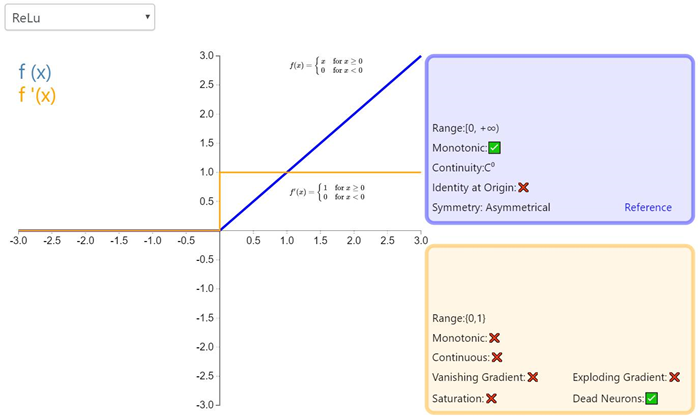
那么你可能会问,「它是线性函数吧?为何我们说它是非线性函数?」
在线代中,线性函数就是两个向量空间进行向量加和标量乘的映射。
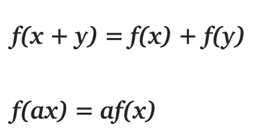
给定上面的定义,我们知道 max(0, x) 是一个分段线性函数。之所以说是分段线性,是因为它在 (−∞, 0] 或 [0,+∞) 上符合线性函数的定义。但是在整个定义域上并不满足线性函数的定义。例如f(−1) + f(1) ≠f (0)
所以 Relu 就是一个非线性激活函数且有良好的数学性质,并且比 sigmoid 和 tanh 都运算得快。除此以外,Relu 还因避免了梯度消失问题而闻名。然而,ReLU 有一个致命缺点,叫「ReLU 坏死」。ReLu 坏死是指网络中的神经元由于无法在正向传播中起作用而永久死亡的现象。
更确切地说,当神经元在向前传递中激活函数输出为零时,就会出现这个问题,导致它的权值将得到零梯度。因此,当我们进行反向传播时,神经元的权重将永远不会被更新,而特定的神经元将永远不会被激活。
还有件事值得一提。你可能注意到,不像 sigmoid 和 tanh,Relu 并未限定输出范围。这通常会成为一个很大的问题,它可能在另一个深度学习模型如递归神经网络(RNN)中成为麻烦。具体而言,由 ReLU 生成的无界值可能使 RNN 内的计算在没有合理的权重的情况下发生数值爆炸。因此反向传播期间权重在错误方向上的轻微变化都会在正向传递过程中显著放大激活值,如此一来学习过程可能就非常不稳定。我会尝试在下一篇博客文章中详细介绍这一点。
Leak ReLU
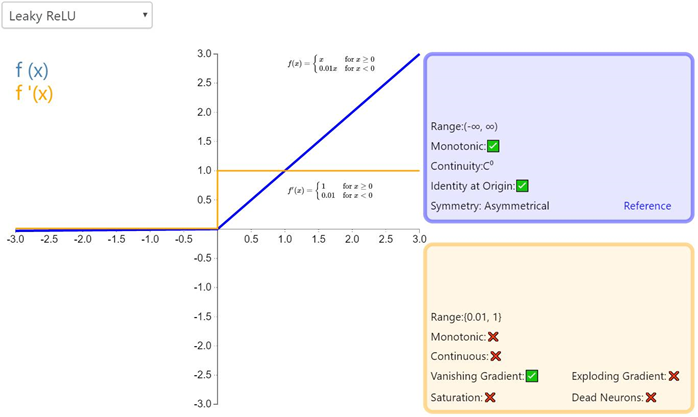
经典(以及广泛使用的)ReLU 激活函数的变体,带泄露修正线性单元(Leaky ReLU)的输出对负值输入有很小的坡度。由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习(虽然会很慢)。
Cos
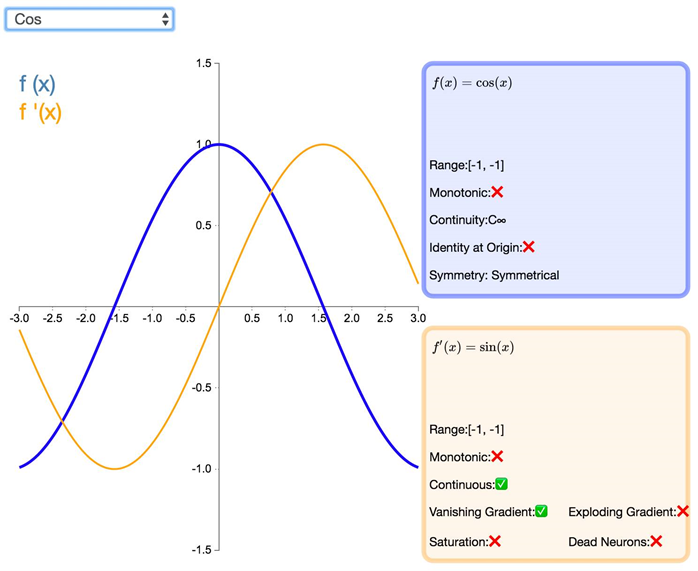
如同正弦函数,余弦激活函数(Cos/Cosine)为神经网络引入了周期性。它的值域为 [-1,1],且导数处处连续。和 Sinusoid 函数不同,余弦函数为不以零点对称的偶函数。
Sinc
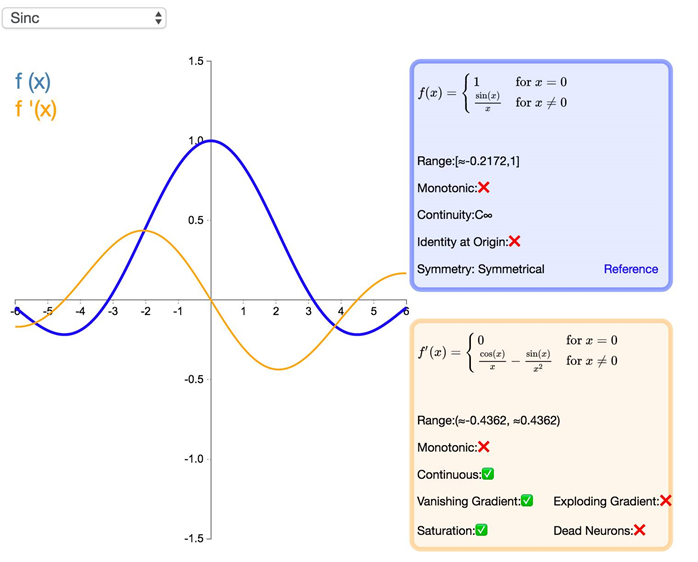
Sinc 函数(全称是 Cardinal Sine)在信号处理中尤为重要,因为它表征了矩形函数的傅立叶变换(Fourier transform)。作为一种激活函数,它的优势在于处处可微和对称的特性,不过它比较容易产生梯度消失的问题。
本文转自 开源中国 - Amui次元,转载此文目的在于传递更多信息,仅作学习交流之用,版权归原作者所有。






