之前上课的时候其实就没搞懂什么是维纳滤波和卡尔曼滤波,老师完全讲不清楚来龙去脉,滤波、预测都说不清楚。后来刷知乎看到大神的解释,当时倒是茅塞顿开,但是前几天做笔试遇到关于维纳滤波的题目,发现功课没做够。要学习一个东西,我认为第一步不应该是讲它的定义,而是先搞清楚它是在上面背景下提出的,伟大的数学家提出一个概念肯定不是为了考我们的,而是为了解决实际问题的。
冈萨雷斯书中第三章和第四章分别讲了空间滤波和频率域滤波,维纳滤波放在了第五章图像复原和重建。第五章其实就是滤波的应用,因为图像有退化,所以才要复原,而要想复原,必须要搞清楚图像退化的过程。一幅图像从镜头捕捉到传输,存储都会产生各种各样的畸变,这些过程统称为退化过程。可以发现,图像退化是相对于两幅图像而言的,一幅是原图,一幅是退化后的图像,图像复原的目的是将退化后的图像变换到尽量接近原图的过程,即退化的逆过程。尽量接近原图就是我们的指标,所以图像复原是一个客观的过程,而图像增强是一个主观的过程,输出图像的指标是人类视觉的接收程度。
数学上,我们把退化过程分成两部分,一个是退化函数H,一个是加性噪声。所以频率域退化模型如下式:
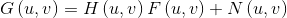
退化函数和噪声有多种组合。关于噪声我们已经很熟悉了,高斯噪声、椒盐噪声、瑞利噪声等。当退化过程只存在噪声时,使用空间滤波,包括均值滤波器和统计排序滤波器。当噪声是周期性时,可以使用频率域滤波消除周期噪声,包括带通、带阻、陷波滤波器。
关于退化函数,我们只能尽量去估计。书中提到了三种方法。图像观察估计是选取图像中信号最强的部分,并认为这部分图像的噪声为0,锐化处理过后就认为得到了复原之后的图像,锐化根据该部分的退化函数估计完整的退化函数;试验估计是通过试验,期望得到和获取退化图像相似的装置,不断地调整试验装置,直至得到的图像尽可能接近退化图像,这时再输入亮点模拟冲激,进一步得到退化函数的冲激函数;建模估计就好比是试验估计的数学版本,通过数学表达式模拟装置,比如Hufnagel在1964年提出的基于大气湍流的模型。
既然我们已经可以估计退化函数,那么就可以根据之前的公式进行逆滤波,简单地除以退化函数,得到:
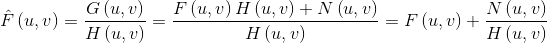
这样,基本估计的退化函数是精确的,我们无法知道噪声分量是多少,这一影响在退化函数H(作为分母)逼近0时尤其严重。一种方法是将退化函数进行截取,在原点附近退化函数值较高,所以可以对退化函数使用低通滤波器进行截取。不进行截取的逆滤波称作全滤波。
前面讲了这么多,终于要过渡到今天的主角了。既然图像复原是一个逼近原图的过程,那么它就可以看作是一个最优化问题,我们可以把策略定为使得复原后的图像和原图的差的平方的期望最小,即均方误差最小。维纳滤波的思想就是把图像和噪声都看作不相关的随机变量,再进行最优化求解。维纳滤波又叫最小均方误差滤波或者最小二乘滤波,它在1942年被提出,当时正值第二次世界大战,运用在了火力跟踪问题中。
链接1推导了一般的SISO信号传播模式下的维纳滤波。
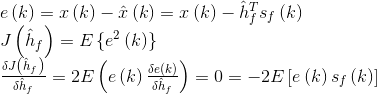
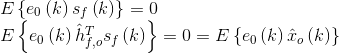
由这个式子就可以得到著名的正交准则推论。上式的意思是误差和估计值(也可以理解为预测值)的乘积的期望为0,也就是它们之间是正交的。

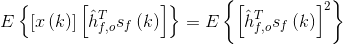
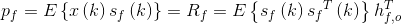
这就是著名的维纳-霍夫wiener-Hopf方程。左边是互相关矩阵,右边是相关矩阵,求Sf的方差。X是原图,Sf是退化后的图像。可以由此求得维纳滤波器的冲激响应。H=Rxx/Rxs
Rxx是观测数据的自相关函数,Rxs是观测数据与期望数据的相关函数。
在之前给出的退化模型中,Rxx=HS,Rxs=SH2+N
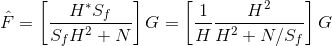
N和Sf就是噪声和信号的功率谱。它们的具体数值很少是已知的,而我们实际也只需要知道它们的比值K,K值的选择是交互式进行选择的。
维纳滤波的缺点就是最后提到的,它需要未退化图像和噪声的功率谱,即便可以人为选择K值,也无法保证是最优解。同时,维纳滤波的最优是平均意义上的最优,意思是维纳滤波对多幅图像处理的结果的平均值是最满意的,但具体到每幅具体的图,不一定是最优的。这就引出来了更进一步的约束最小二乘方滤波。
Reference:
推导https://blog.csdn.net/qq_23660243/article/details/80203987
电子科大课件https://blog.csdn.net/orangehdc/article/details/39992829
来源:CSDN ,作者:zcg1942
原文:https://blog.csdn.net/zcg1942/article/details/82463621




