梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一。
在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。
一般情况下,我们把要最小化或最大化的函数称为目标函数。当我们队其进行最小化时,我们也把他称为代价函数,损失函数或误差函数。
我们说导数对于最小化一个函数很有用,因为它告诉我们如何更改x来略微地改善y。加入,我们知道对于足够小的\varepsilon来说,
f(x-\varepsilonsign(f'(x)))<f(x)。因为我们可以将x往导数的反方向移动一小步来减少f(x)。这种技术被称为梯度下降。
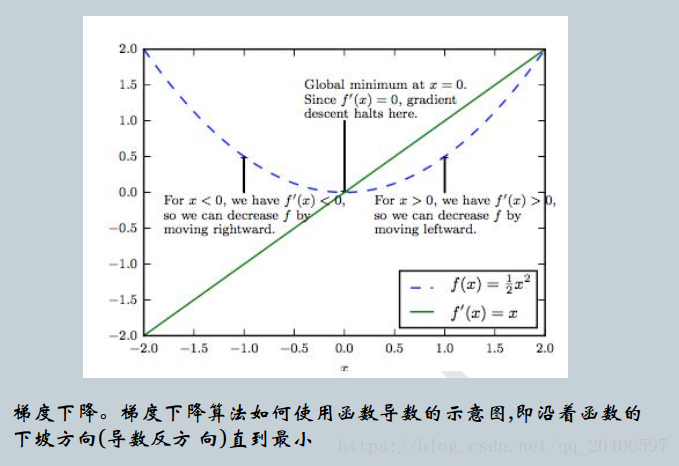
梯度下降寻找的是loss function的局部极小值,而我们想要全局最小值。如下图所示,我们希望loss值可降低到右侧深蓝色的最低点,但loss在下降过程中有可能“卡”在左侧的局部极小值中方,也有最新研究表明在高维空间下局部极小值通常很接近全局最小值,训练网络时真正与之“斗争”的是鞍点。但不管是什么,其难处就是loss“卡”在了某个位置后难以下降。唯一的区别是,陷入局部极小值就难以出来,陷入鞍点最终会逃脱但是耗时。
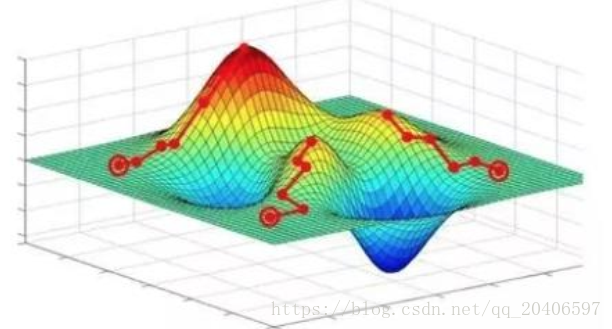
试图解决“卡在局部极小值” 问题的方法分为两大类:
(1)随机梯度下降:每次只更新一个样本所计算的梯度。
(2)小批量梯度下降:每次更新若干样本所计算的梯度的平均值。
(3)动量:不仅仅考虑当前样本所计算的梯度;Nesterov动量;Momentum的改进。
(4)Adagrad, RMSProp, Adadelta:这些方法都是训练过程中依照规则降低学习速率,部分也综合了动量。
优化注意事项: 合理初始化权重,预训练网络,使网络获得一个较好的“起始点”。
常用的初始化权重的方法:高斯分布初始权重,均匀分布初始权重,Glorot初始权重,He初始权,稀疏矩阵初始权重。
本文转自:CSDN - 沐尔还吃的博客,转载此文目的在于传递更多信息,版权归原作者所有。
原文链接:https://blog.csdn.net/qq_20406597/article/details/81145293






