1. 背景:
1801年,意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后,由于谷神星运行至太阳背后,使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星,但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中,而法国科学家勒让德于1806年独立发现“最小二乘法”,但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。
1829年,高斯提供了最小二乘法的优化效果强于其他方法的证明,见高斯-马尔可夫定理。
2. 最小二乘法在机器学习中被用来
3. 高中关于最小二乘法估计
概括:
假设有若干个样本点 ( x1 , y1 ) , ( x2 , y2 ) , ( x3 , y3 ) , ( x4 , y4 ) , ( x5 , y5 ) , 求解直线y=kx+b,是的这些样本点到直线的距离最小。
我们高中的求解方式也是这样的:

展开为:
min_sum = [ y1- ( kx1+b )]^2 + [ y2- ( kx2+b ) ]^2 + [ y3- ( kx3+b ) ]^2 + [ y4- ( kx4+b ) ]^2 + [ y5 - ( kx5+b ) ]^2
就是各个点到我们设定的直线的欧式距离
化简为:
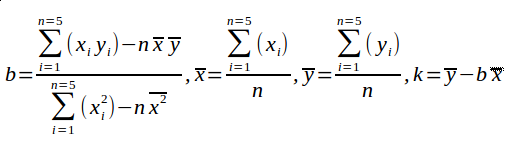
以上就是我们高中对于最小二乘法的最初认知。这个求解的过程,我们称之为最小二乘法,而求解的这条直线,我们称之为线性回归,线性回归用来近似的预测数据的真是情况.
举个例子:(此题来自:北师大版高中数学)
从某所高中随机抽取一些可爱的萌妹子,就比如6个女生好了,测出她们的体重和身高如下表,现在来了一个60kg的女生,求问它的身高会有多高?

用python画图来表示这些数据好了:
# encoding: utf8 import matplotlib import matplotlib.pyplot as plt from matplotlib.font_manager import FontProperties from sklearn.linear_model import LinearRegression from scipy import sparse print matplotlib.matplotlib_fname() # 将会获得matplotlib包所在文件夹 font = FontProperties() plt.rcParams['font.sans-serif'] = ['Droid Sans Fallback'] # 指定默认字体 plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题 plt.figure() plt.title(u' 可爱女生的数据 ') plt.xlabel(u'x 体重') plt.ylabel(u'y 身高') plt.axis([40, 80, 140, 200]) plt.grid(True) x = [[48], [57], [50], [54], [64], [61], [43], [59]] y = [[165], [165], [157], [170], [175], [165], [155], [170]] plt.plot(x, y, 'k.') model = LinearRegression() model.fit(x, y) # y2 = model.predict(x) # plt.plot(x, y2, 'g-') plt.show()
散点图:
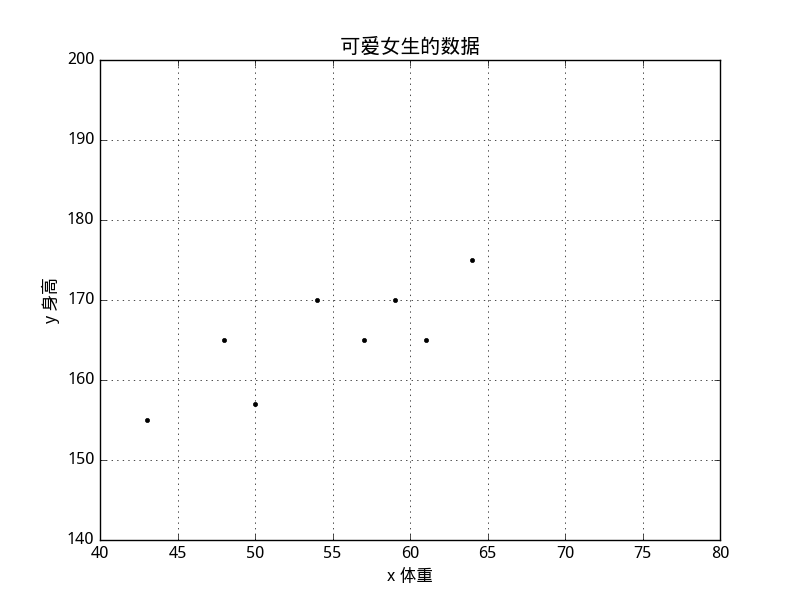
对于这个例子,我们可以使用上面的公式,求解出回归方程,并可以得到方程拟合的该女生的身高值,但是这太麻烦了 , 毕竟高中还是太too yong too simple了~
4. 大学关于最小二乘法
基于上面的那个问题,我们大学有没有更好的一点的求解方式 ?
4.1 大学对于最小二乘法的概括:
找到那样一条函数曲线使得观测值的残差平方之和最小。通俗的讲:见高中部分概括
4.2 继续上面的这个问题思路:
我们已知这些数据:
f(x,y) = [y1- (kx1+b)]^2+[y2- (kx2+b)]^2+[y3- (kx3+b)]^2+[y4- (kx4+b)]^2+[y5- (kx5+b)]^2+[y6- (kx6+b)]^2+[y7- (kx7+b)]^2+[y7- (kx7+b)]^2
如果存在最大值,那么只需要满足f(x,y)对于x,y的一阶偏导数均为0
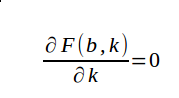
求解得:
k= 0.849 , b =85.172
所以预测值为:
y = 0.849x - 85.172 将y = 60kg 代入求解得: x = 170.99175
我们再使用Python求解一次:
# encoding: utf8
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from scipy.optimize import leastsq
from sklearn.linear_model import LinearRegression
from scipy import sparse
import numpy as np
# 拟合函数
def func(a, x):
k, b = a
return k * x + b
# 残差
def dist(a, x, y):
return func(a, x) - y
font = FontProperties()
plt.rcParams['font.sans-serif'] = ['Droid Sans Fallback'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
plt.figure()
plt.title(u' 可爱女生的数据 ')
plt.xlabel(u'x 体重')
plt.ylabel(u'y 身高')
plt.axis([40, 80, 140, 200])
plt.grid(True)
x = np.array([48.0, 57.0, 50.0,54.0, 64.0, 61.0, 43.0, 59.0])
y = np.array([165.0, 165.0,157.0, 170.0, 175.0, 165.0, 155.0, 170.0])
plt.plot(x, y, 'k.')
param = [0, 0]
var= leastsq(dist, param, args=(x, y))
k, b = var[0]
print k, b
plt.plot(x, k*x+b, 'o-')
plt.show()
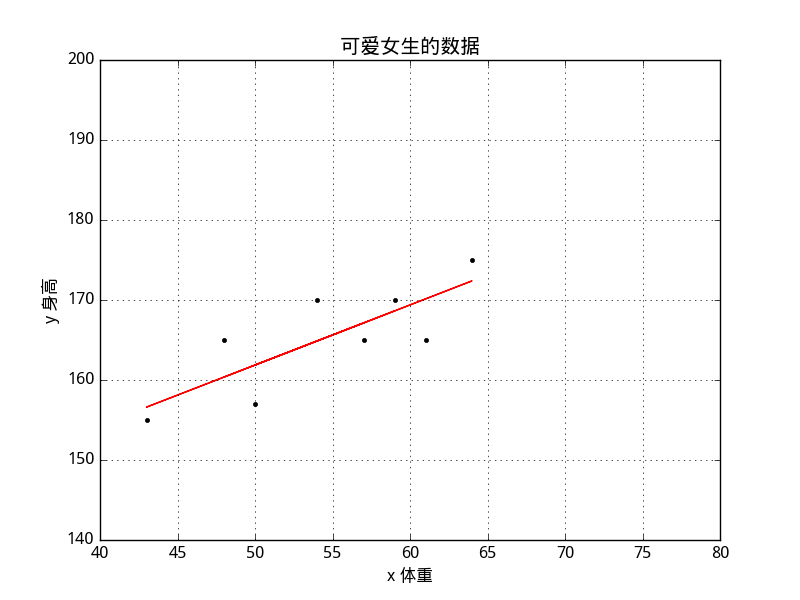
从图中,可以发现结果大致相符。
转自:Gxjun,转载此文目的在于传递更多信息,版权归原作者所有。
