0、思想:
对于给定的待分类项x,通过学习到的模型计算后验概率分布,即:在此项出现的条件下各个目标类别出现的概率,将后验概率最大的类作为x所属的类别。后验概率根据贝叶斯定理计算。
关键:为避免贝叶斯定理求解时面临的组合爆炸、样本稀疏问题,引入了条件独立性假设。用于分类的特征在类确定的条件下都是条件独立的。
1、朴素贝叶斯朴素在哪里?
简单来说:利用贝叶斯定理求解联合概率P(XY)时,需要计算条件概率 P( X | Y ) 。在计算 P ( X | Y ) 时,朴素贝叶斯做了一个很强的条件独立假设(当Y确定时,X的各个分量取值之间相互独立),即 P ( X1 = x1 , X2 = x2 , ... Xj=xj|Y=yk ) = P ( X1 = x1 | Y = yk ) * P( X2 = x2 | Y = yk ) * ... * P ( Xj = xj | Y = yk ) 。
主要的应用:电子邮件垃圾过滤、新闻分类
• 在训练朴素贝叶斯分类器之前,要处理好训练集,文本的清洗还是有很多需要学习的东西;
• 根据提取的分类特征将文本向量化,然后训练朴素贝叶斯分类器。
• 去高频词汇数量的不同,对结果也是有影响的的。
• 拉普拉斯平滑对于改善朴素贝叶斯分类器的分类效果有着积极的作用。
2、朴素贝叶斯与LR的区别?
简单来说:
(1)朴素贝叶斯是生成模型,根据已有样本进行贝叶斯估计学习出先验概率P(Y)和条件概率 P ( X | Y ),进而求出联合分布概率 P ( X Y ),最后利用贝叶斯定理求解 P ( Y | X ), 而LR是判别模型,根据极大化对数似然函数直接求出条件概率P ( Y | X ) ;
(2)朴素贝叶斯是基于很强的条件独立假设(在已知分类Y的条件下,各个特征变量取值是相互独立的),而LR则对此没有要求;
(3)朴素贝叶斯适用于数据集少的情景,而LR适用于大规模数据集。
前者是生成式模型,后者是判别式模型,二者的区别就是生成式模型与判别式模型的区别。
1)首先,Navie Bayes通过已知样本求得先验概率 P ( Y ) , 及条件概率 P( X | Y ) , 对于给定的实例,计算联合概率,进而求出后验概率。也就是说,它尝试去找到底这个数据是怎么生成的(产生的),然后再进行分类。哪个类别最有可能产生这个信号,就属于那个类别。
优点:样本容量增加时,收敛更快;隐变量存在时也可适用。
缺点:时间长;需要样本多;浪费计算资源
2)相比之下,Logistic回归不关心样本中类别的比例及类别下出现特征的概率,它直接给出预测模型的式子。设每个特征都有一个权重,训练样本数据更新权重w,得出最终表达式。梯度法。
优点:直接预测往往准确率更高;简化问题;可以反应数据的分布情况,类别的差异特征;适用于较多类别的识别。
缺点:收敛慢;不适用于有隐变量的情况。
3、 在估计条件概率 P( X | Y ) 时出现概率为0的情况怎么办?
简单来说:引入 λ ,当 λ = 1 时称为拉普拉斯平滑。
4、 朴素贝叶斯的优缺点
优点:对小规模的数据表现很好,适合多分类任务,适合增量式训练。
缺点:对输入数据的表达形式很敏感(离散、连续,值极大极小之类的)。
5、为什么属性独立性假设在实际情况中很难成立,但朴素贝叶斯仍能取得较好的效果?
1)对于分类任务来说,只要各类别的条件概率排序正确、无需精准概率值即可导致正确分类;
2)如果属性间依赖对所有类别影响相同,或依赖关系的影响能相互抵消,则属性条件独立性假设在降低计算开销的同时不会对性能产生负面影响。
6、为什么要后验概率最大化:
等价于期望风险最小化。假设选取0-1损失函数,即分类正确取1,错误取0,这时的期望风险最小化为
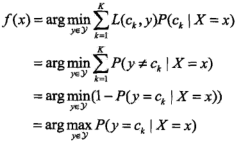
7、算法问题:
实际项目中,概率值往往是很小的小数,连续微小小数相乘容易造成下溢出使乘积为0.
解决方法:对乘积取自然对数,将连乘变为连加。
另外需要注意:给出的特征向量长度可能不同,这是需要归一化为通长度的向量(这里以文本分类为例),比如说是句子单词的话,则长度为整个词汇量的长度,对应位置是该单词出现的次数。
8、先验条件概率的计算方法:
a.离散分布时:统计训练样本中每个类别出现的频率。若某一特征值的概率为0会使整个概率乘积变为0(称为数据稀疏),这破坏了各特征值地位相同的假设条件。
解决方法一:采用贝叶斯估计( λ = 1 时称为拉普拉斯平滑):
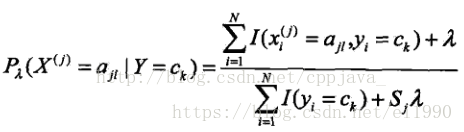
解决方法二:通过聚类将未出现的词找出系统关键词,根据相关词的概率求平均值。
b.连续分布时:假定其值服从高斯分布(正态分布)。即计算样本均值与方差。
本文转自:博客园 - 深度机器学习,转载此文目的在于传递更多信息,版权归原作者所有。
