本文延续该系列的上一篇 深度学习优化函数详解(0)– 线性回归问题。
上一篇讲到了最基本的线性回归问题,最终就是如何优化参数 a, b 寻找最小的 loss
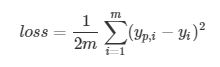
显然loss函数是一个二次函数,问题就转化成了如何求二次函数的最小值。我们再举一个更简单的例子,假设我们要优化的函数是 y = x2,初始条件我们选择了x0 = 2,y0 = 4,画在图上如下:
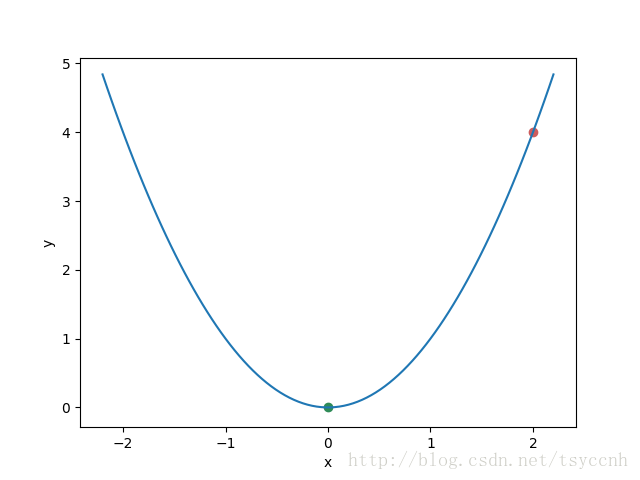
图中红色的点就是我们的初始点,很显然,我们想要找的最终最优点是绿色的点 ( 0 , 0 )。
接下来我们需要对目标函数求微分
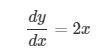
这就是所谓的梯度,当 x =2 的时候,可以求得该点的梯度为4,翻译成人话就是当前这一点的’倾斜程度’是4。下面举几个例子
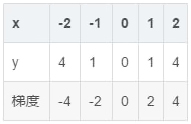
和上面的图一对应就很明显了,梯度的绝对值越大,数据点所在的地方就越陡。数字为正数时,越大,表示越向右上方陡峭,反之亦然。好了,懂了什么是梯度,下面我们就来聊聊梯度下降是个什么玩意。现在我们先假设我们自己就是一个球,呆在图中的红点处,我们的目标是到绿点处,该怎么走呢?很简单,顺着坡 向下走就行了。现在球在 ( 2 , 4 ) 点处,这一点的倾斜程度是4,向右上方陡峭。接下来要做的就是向山下走,那么每一次走多远 呢?先小心一点,按当前倾斜程度的1%向下走。也就是xnew=x0−0.01∗4, xnew=1.96 再算一下 y 值等于多少 ynew=3.8416 < 4。小球成功的往下滚了一点,这样一直滚下去,最终就会滚到绿色的点,如下图
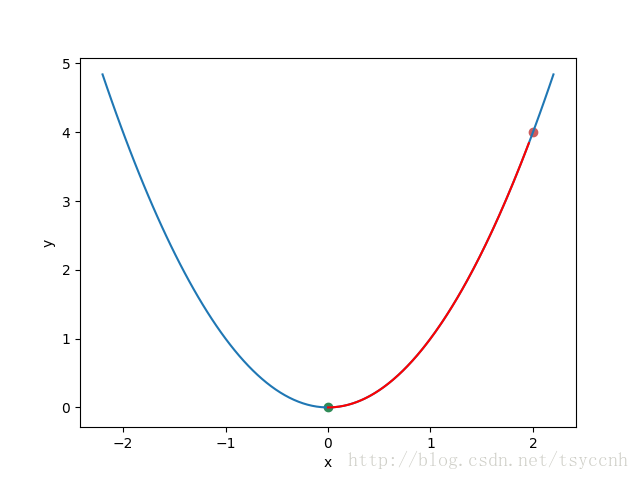
红色的曲线表示了小球的滚动路线
这就是梯度下降法
转换成数学语言就是在每一次迭代按照一定的学习率 α 沿梯度的反方向更新参数,直至收敛,公式
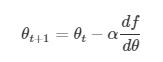
接下来我们回到房价预测问题上。
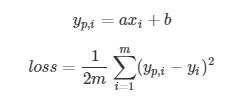
将上面两个方程合并, 并把1/2放到右边方程
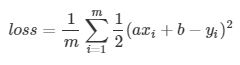
一共有m项累加,我们单拿出来一项来分析。
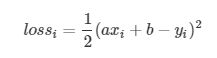
要优化的参数有两个,分别是a和b,我们分别对他们求微分,也就是偏微分
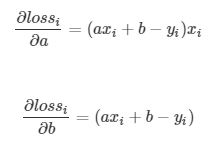
这里我们看到了loss函数为什么要在前面加一个1/2,目的就是在求偏微分的时候,可以把平方项中和掉,方便后面的计算。
自然地我们将每一个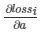 和
和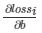 累加起来得到
累加起来得到
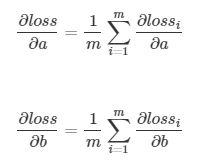
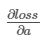 记为
记为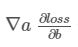 记为 ∇b ,分别表示 loss 在 a、b 方向的梯度, 更新参数的方法如下
记为 ∇b ,分别表示 loss 在 a、b 方向的梯度, 更新参数的方法如下
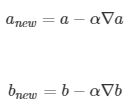
实验
写了这么多公式,是时候直观的看一看梯度下降法是怎么一回事了。下面将绘制四幅图,分别是
1. 在a,b的一定的取值范围内,计算所有的loss,绘制出分布图
2. 将这张分布图拍扁,画出等高线图
3. 绘制原始的数据折线以及依据a,b绘制预测直线
4. 绘制在训练过程中loss的变化
如下

我们看到图1和之前二次函数的那个例子很像,只不过是在三维空间内的一个曲面,初始的参数选择 a = 15 , b = 10,可以看到图1上曲面右侧有一个浅浅的点,就是初始值了。图二是等高线图,俯视更加明显,等高线图主要是为了之后训练的过程中可视化更清晰。图三上方的绿线是根据选择的初始值绘制的,下方是真实的实验数据,可以看出差距很远,需要优化的步骤还很多。将学习率 α 设置为0.01, 经过200次迭代,结果如下图

图一和图二都可以很直观的看到loss的减小。图三也从模型上给出了最终逼近的过程。图四可以看出下降还是很快的。
值得注意的是,不同的学习率对算法的收敛速度影响很大,下图是 α = 0.15 的结果

基本在前10次迭代就快速收敛。
但是如果学习率设置的太大的话,很容易造成发散。说白了就是步子迈的太大了,一步迈到对面更高的山坡上去了,结果越迈越高,最后就不知道跑到哪里去了,如下图 ( α = 0.3 )
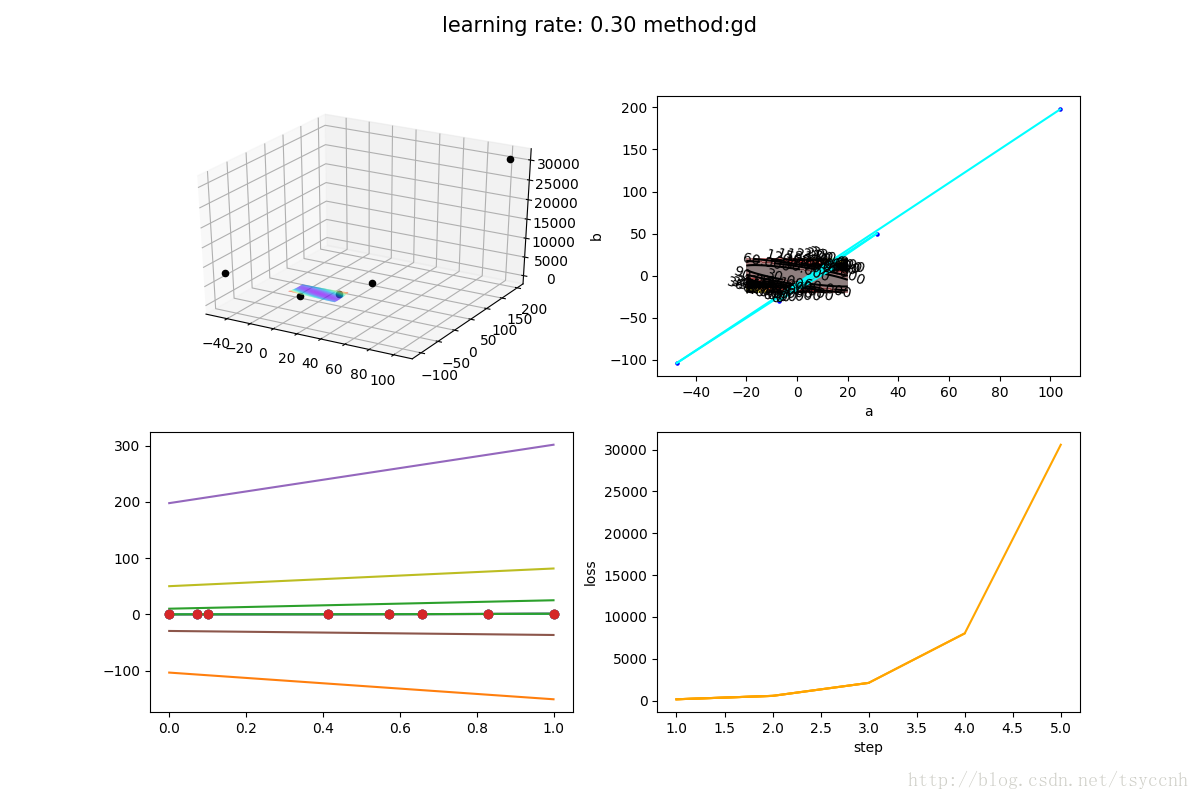
每个图请注意看坐标轴的尺度,都大的不行,一开始的画的曲面和和等高线图都变得十分小,而这也只是迭代了5步而已。
所以机器学习里面,参数的选择是个技术活,往往同一个模型,两个人调参,结果却大相径庭。
本文的源码在此: https://github.com/tsycnh/mlbasic/blob/master/p1%20gradient%20descent.py
本文转自:CSDN - 史丹利复合田,转载此文目的在于传递更多信息,版权归原作者所有。
