使用蒸馏法对低精度推理的浮点网络进行高保真转换

作者：Szabolcs Cséfalvay

神经网络加速器快速、低功耗推理的一个主要挑战是模型的大小。近年来，随着模型尺寸的增加，推理时间和每次推理能耗的相应增加，神经网络向更深的神经网络发展，激活和系数也在增加。这在资源受限的移动和汽车应用中尤为重要。低精度推理有助于通过降低 DRAM 带宽（这是影响设备能耗的一个重要因素）、计算逻辑成本和功耗来降低推理成本。

在这种情况下，下面的问题自然而然地出现了：编码神经网络权重和激活的最佳位深度是多少？有几个建议的数字格式可以减少位深度，包括Nvidia的TensorFloat，谷歌的8位非对称定点（Q8A）和bfloat16。但是，虽然这些格式是朝着正确方向迈出的一步，但不能说它们是最佳的：例如，大多数格式都为要表示的每个值存储一个指数，当多个值在同一区间时，这些指数可能是多余的。更重要的是，他们没有考虑神经网络的不同部分通常有不同的位深度要求这一事实。有些图层可以用较低的位深度编码，而其他图层（如输入和输出层）需要更高的位深度。MobileNet v3就是一个例子，它可以从 32 位浮点转换为大多数在 5-12 位区间内的位深度（见图 1）。

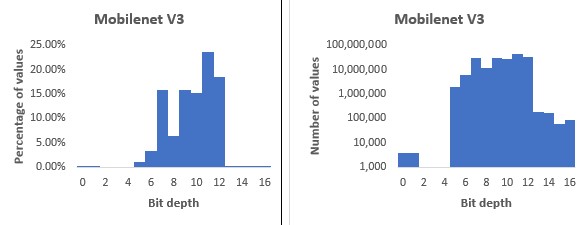
我们称使用不同的位深度来编码原始浮点网络的不同部分为可变位深度 （VBD） 压缩。

当然，权重的位深度编码和网络准确度也是需要权衡的。较低的位深度会导致更有效的推断，但删除过多的信息会损害准确性，这意味着需要找到一个最佳的折中方案。VBD 压缩的目标是在压缩和精度之间进行平衡。原则上，可以将其视为优化问题：我们希望用尽可能少的比特数达到最佳精度的网络。这是通过在损失函数中添加新的一项来实现的，该项表示网络的大小，以便可以沿原始损失函数最小化，该函数可以大致表示为：

总损失 = 网络错误 + γ（网络大小）

其中γ是一个权重因子，用于控制网络大小和误差之间的目标权衡。

因此，要以这种方式压缩网络，我们需要两件事：精度的可微度量（错误）和网络大小的可微度量（压缩位深度）。网络大小项和网络误差项相对于比特数的可微性非常重要，因为它使我们能够优化（学习）比特深度。

可微网络规模

对于可微量化，我们可以使用任何具有可微位深度参数的函数，该参数将一个或多个浮点值映射为硬件可表示的压缩数字格式。例如，我们可以使用 Google Q8A 量化的可变位深度版本（其中可表示范围不是以零为中心）：

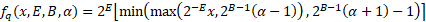
其中：

• ⌊x⌉是 x 四舍五入到最近的整数（使用目标硬件平台的舍入模式）
• B 是位深度。
• E 是浮点表示的指数。
• α 是不对称参数。

手动测试链接

在实践中，量化参数 B、E 和α用于压缩多个权重，例如，单个参数用于压缩整个神经网络层（激活或权重张量）或层内的通道。

我们还可以通过将不对称参数设置为 0 来使用对称量化（有效地将其转换为缩放的 B位无符号整数格式）：

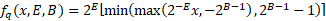
为了实现对所有参数的反向传播，我们使用直通估计器，将圆形函数的梯度作为 1。这使得公式中的所有操作都是可微的，使所有参数（包括位深度）都可学习！

此时，我们可以选择要训练的参数：
1. 权重和最大压缩位深度。
2. 只有权重和指数（对于固定的位深度）。
3. 只有量化参数，它有几个好处（如下所述），成本可能更低的压缩比。

在生成本文的结果时选择了选项 3。

另一个需要考虑的方面是优化位深度参数 B（对于某些格式的指数 E）：任何硬件都需要 B 是整数。要找到整数解，我们有多种选择：

• 将四舍五入与直通估计器一起应用于 B 参数（例如，使用公式）。但是，这给优化表面带来了不连续性，虽然可以处理，但超出了本文的范围。
  
  
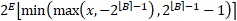
• 这里选择的替代方案是在训练的第一阶段优化浮点数B，"保守"地将其四舍五入到最近的整数⌈B⌉（ 否则激活和权重张量的重要部分可能会被钳制），将其固定为常量并继续训练。这样平均会损失大约 0.5 位的潜在压缩，但保证不会发生不适当的裁剪。

可微精度测度

为了测量网络的准确性，我们可以简单地使用网络最初训练的相同损失函数。然而，在许多应用中，目标是压缩一个已经用32 位浮点训练的网络，这意味着我们可以用蒸馏损失代替。这意味着压缩网络的精度是根据原始网络的输出来衡量的。在这项工作中，选择（输出）logits之间的绝对差异作为蒸馏损失，但也可以采用其他措施。

使用的蒸馏损失定义为：

（等式1）

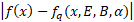
请参阅图 2 以说明这一点。

图2：用于压缩的蒸馏损失的可视化。

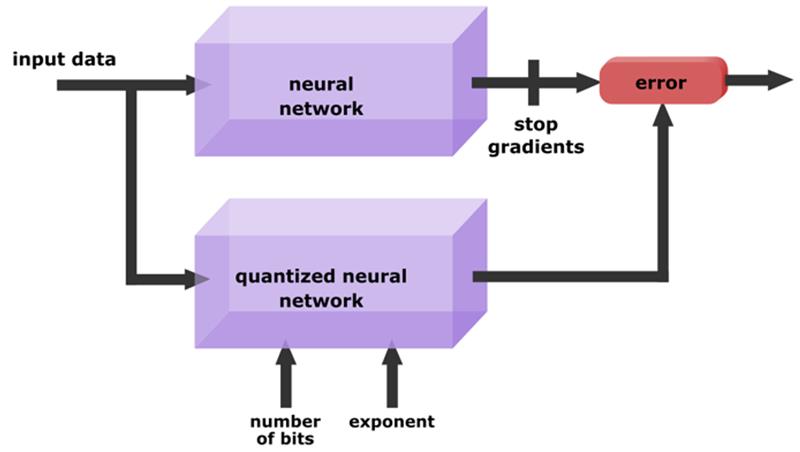
蒸馏损失有许多优点：

• 无标签训练：我们不需要标签数据来压缩网络，因为我们用原始网络的输出取代了标签。这意味着我们可以压缩网络，而无需访问（可能是专有的）原始数据集：我们只需要具有代表性的输入和原始网络。
• 通用性：神经网络压缩机具有通用性：它不需要特定于网络。
• 更少的训练数据：由于我们只是训练量化参数，过度拟合的范围大大缩小，所以我们可以使用更少的训练数据。有时候一张图片就足够了！
• 软目标：由于从输入得到的蒸馏损失比标签包含更多的量化误差信息，因此它允许更快、更准确的收敛。
• 我们可以使用蒸馏损失将权重与量化参数一起训练。然而，在这种情况下，我们需要更多的训练数据来防止过度拟合。两全其美的方法是以很小的学习率来训练权重，并提前停止。这样，权重可以抵消量化误差，而不会过度拟合数据集。

可微压缩

将通用的、可微的精度度量与可微量化相结合，得到可微压缩的损失函数：

（等式2）

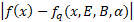
第一个项是误差，第二项是网络大小的成本。B 是网络的平均位深度，可根据整个网络的深度参数来计算：

（等式3）

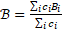
其中c_i是使用位深度参数B_i量化的网络参数（权重或激活）的数量。请注意，此测量方式取决于批次大小。例如，如果对32个批次网络进行评估，则激活张量的大小实际上比使用1 批次大小的高出 32 倍。如果目标是将网络权重存储在尽可能小的空间中，则此指标中也可以忽略激活。

选择量化粒度

一些神经网络表示，如谷歌的Q8A格式，允许将不同的比例系数（与上面的指数E的2次幂相关）应用于权重张量（过滤器）的不同通道。这种更精细的粒度可提高给定压缩级别的网络精度。通过对每个通道应用单独的 E 和α参数，同时对整个张量使用相同的 B 参数，可以通过可变位深度压缩实现相同的目标。然而，每个通道的量化会导致更慢的收敛，因此根据我们的经验，使用学习前张量参数的训练阶段更快，然后将这些参数分解为每通道参数，并让它们在另一个训练阶段收敛。

这最终导致三个阶段的训练计划：

• 根据张量训练所有量化参数
• 切换到每通道指数和移位参数
• 将位深度舍入到整数，并将其固定到常量，然后训练指数和移位参数α。此外，权重也以较小的学习率进行训练。

结果

对象分类

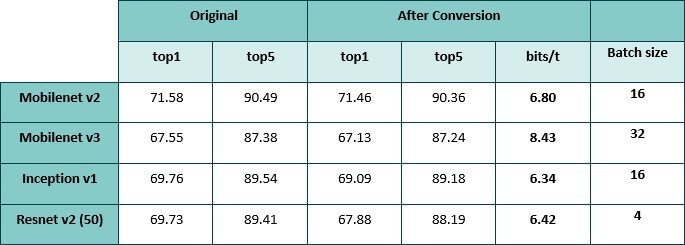
压缩分类网络的精确度。图 1 中的 Mobilenet v3 直方图是不同（较短）训练的结果，与此表中的网络相比，压缩程度较低。

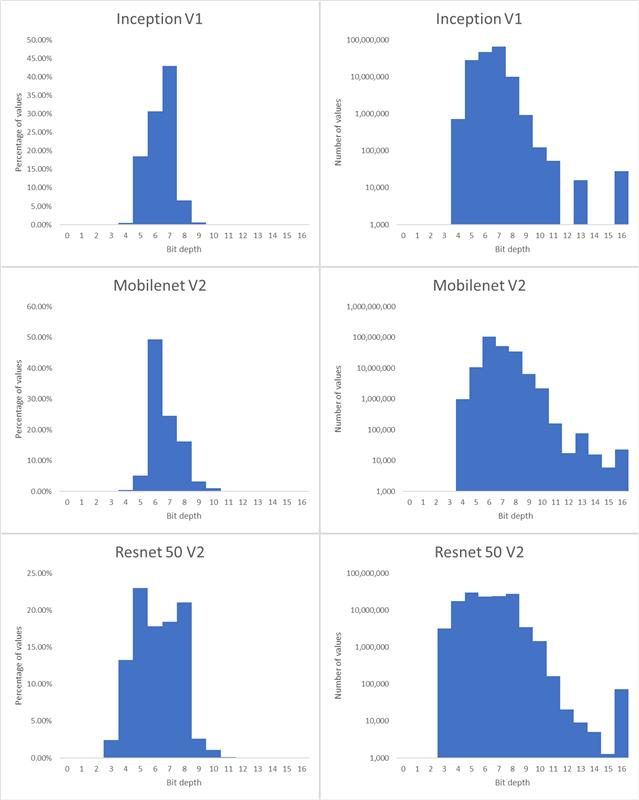
下面显示了此表中选定网络的位深度直方图。

图像分割

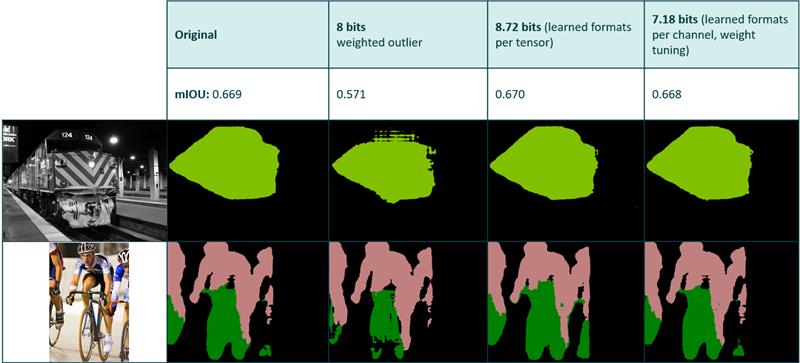
应用于分割网络的不同压缩方法之间的比较。第二个列基于启发式算法，该算法试图在不使用反向传播的情况下确定固定位深度的最佳指数。

风格转换

最后一列使用上述启发式给出10 比特时的完全空白输出。

结论

用于编码神经网络权重和激活的位深度对推理性能有显著影响。将大小精度权衡作为损失函数的一部分，可以在神经网络训练过程中学习任意粒度的最佳比特深度。此外，当优化将 0 位分配给网络的一部分时，它会有效地从架构中删除该部分，作为一种架构搜索，从而降低计算成本和带宽成本。今后的工作将探索这方面的可微网络压缩。

我们提出了一种基于微分量化和蒸馏的通用而灵活的方法，允许在不影响精度的情况下为各种任务优化位数。我们的方法有几个优点，包括训练时间短，重复使用训练过的网络，不需要标签，可调整的大小精度权衡和问题无关的损失功能。通过这种方式，我们可以将网络压缩为有效的可变位深度表示，而不牺牲对原始浮点网络的保真度。

[i] https://blogs.nvidia.com/blog/2020/05/14/tensorfloat-32-精确格式/
[ii]https://www.tensorflow.org/lite/performance/quantization_spec
[iii]https://arxiv.org/abs/1905.12322
[iv] https://arxiv.org/abs/1308.3432
[v]https://arxiv.org/abs/1503.02531

原文链接：https://www.imaginationtech.com/blog/low-precision-inference-using-disti...

声明：本文为原创文章，转载需注明作者、出处及原文链接。