遗传算法原理
遗传算法(Genetic Algorithms)是1962年由美国Michigan大学Holland教授提出的模拟自然界遗传机制和生物进化论而形成的一种并行随机搜索最优化方法。它把自然界中的“优胜劣汰,适者生存”的生物进化原理引入优化参数形成的编码串联群体中,按照所选择的适应度函数并通过遗传中的选择、交叉和变异对个体进行筛选,是适应值好的个体被保留,适应度差的个体倍淘汰,新的种群集成上一代的信息,有优于上一代。这样反复循环,直到满足条件。
遗传算法基本的操作分为:
1. 选择操作
选择操作是指从旧的群体中以一定的概率选择个体到新的群体中,个体被选中的概率是跟适应度值有关,个体适应度值越好,被选中的概率越大。
2. 交叉操作
交叉操作是指从个体中选择两个个体,通过两个染色体的狡猾组合,来查省心的优秀个体。交叉过程为从种群中任选两个染色体,随机选择一点或多点染色体未知进行交换。
3. 变异操作
变异操作是指从种群中任选一个个体,选择染色体的一点进行变异以产生更优秀的个体。
遗传算法具有高效启发式搜索、并行计算等特点,目前已经应用在函数优化、组合优化以及生产调度等方面。
遗传算法的基本要素
遗传算法的基本要素包括染色体编码方法、适应度函数、遗传操作和运行参数。
其中染色体编码方法是指个体的编码方法,目前主要包括二进制法、实数法等。二进制法是指把个体编码成一个二进制串,实数法是指把个体编码成一个实数串。
适应度函数是指根据进化目标编写的计算个体适应度值得函数,通过适应度函数计算每一个个体的适应度值,提供给选择算子进行选择。
遗传操作是指选择操作、交叉操作、和便已操作。
运行参数是遗传算法在初始化时确定的参数,主要包括群体大小M ,遗传代数G ,交叉概率 Pc 和变异概率 Pm
算法流程
遗传算法优化BP神经网络分为BP神经网络结构确定、遗传算法优化和BP神经网络预测3个部分。其中,BP神经网络的结构确定部分根据拟合函数输入输出参数个数确定BP神经网络结构,进而确定遗传算法个体的长度。遗传算法优化使用遗传算法优化BP神经网络的权值和阈值,种群中的每个个体都包含了一个网络所有的权值和阈值,个体通过适应度函数计算个体的适应度值,遗传算法通过选择、交叉和变异操作找到最优适应度值对应个体。BP神经网络预测用遗传算法得到最优个体对网络初始权值和阈值赋值,网络经训练后预测函数输出。

遗传算法的实现
1. 种群初始化
个体编码方法为实数编码,每隔个体均为一个实数串,由输入层和隐含层连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值4个部分组成。个体包含了神经网络全部的权值和阈值,在网路结构一直的情况下,就可以构成一个结构、权值、阈值确定的神经网络。
2. 适应度函数
根据个体得到BP神经网络的初始权值和阈值,用训练数据训练BP神经网络后预测系统输出,把预测输出个期望的输出之间的误差绝对值和 E 作为个体适应度值F计算公式为

式中,n 为网络输出节点数;yi 为BP神经网络第 i 个节点的期望输出 oi 为第 i 个节点的实际输出;k 为系数。
3. 选择操作
遗传算法选择操作有轮盘赌法、锦标赛法等多种方法。选择轮盘赌法时,即基于适应度比例的选择策略,每个个体 i 的选择概率 pi 为:

式中,Fi 为个体 i 的适应度值,由于适应度值越小越好,所以在个体选择前对适应度求倒数;k为系数;N为种群个体数目。
4. 交叉操作
由于个体采用实数编码,所以交叉操作方法采用实数交叉法,第 k 个染色体ak 和第l个染色体a_l在j为的交叉操作方法如下:
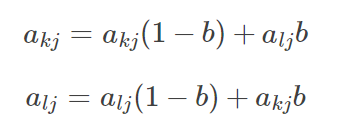
式中,b是[0,1]之间的随机数。
5. 变异操作
选取第 i 个个体的第j个基因 aij 进行变异变异操作方法如下:
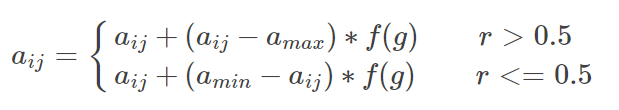
式中,amax为基因 aij 的上界;amin 为基因的下界;f ( g ) = r2( 1 − g/Gmax)2r2 是一个随机数;g 为当前迭代次数;Gmax是最大的进化次数;r为[0,1]间的随机数。
版权声明:本文为CSDN博主「wly2014」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/u014271114/article/details/53445701






