机器学习算法一般都会有训练和测试的过程，而且算法在不同训练集（训练集来自同一个分布）上学得的模型，测试的结果也很可能不同。
一般来说，算法的方差衡量了训练集的变动导致的模型性能的变化，即多次训练的模型之间的性能差异性。偏差则是度量算法的期望输出与真实标记的区别，表达了学习算法对数据的拟合能力。而噪声则表示数据的真实标记与数据在数据集上标记的区别，表明算法在当前任务上能达到的测试误差的下界。
假设数据集用 D 表示，测试样本 x，y 表示 x 在数据集上的标记，y~表示xx的真实标记，f( x ; D ) 表示从训练集 D 上学得的模型 f 的预测输出。
令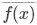
表示从不同训练集上学得模型的期望输出，则
则可以定义方差、偏差和噪声的表达，
方差为：
偏差为：
噪声为：
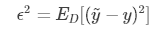
如果对期望泛化误差进行分解，可以得到
即算法的期望泛化误差可以分解为偏差、方差和噪声之和。
另外，一般来说，如果泛化误差的下界为0%，则高方差和高偏差对应如下几种情况。
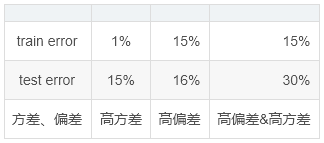
在机器学习中，针对高方差和高偏差的情况，处理机制也是完全不一样的。首先要确保算法有足够的拟合能力，能够很好地处理该任务，即降低偏差，而这通常需要更换算法或者调优算法。在达到低偏差后，如果存在高方差，则需要通过获取更多的训练数据或正则化或dropout等机制减少方差。
另外，在集成学习中，bagging一般可以用来减少方差，而boosting则有利于减小偏差。
版权声明：本文为CSDN博主「keep_forward」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/b876144622/article/details/81048335
