模型过于简单必然导致偏差过大,过于复杂必然导致方差过大
a、欠拟合:偏差过大,做特征工程、减小(弱)正则化系数;
b、过拟合:方差过大,可增加样本、减少特征、增加(强)正则化系数;
1、模型偏差bias
偏差是指预测结果与真实值之间的差异,排除噪声的影响,偏差更多的是针对某个模型输出的样本误差,偏差是模型无法准确表达数据关系导致,比如模型过于简单,非线性的数据关系采用线性模型建模,偏差较大的模型是错的模型;
2、模型方差variance
模型方差不是针对某一个模型输出样本进行判定,而是指多个(次)模型输出的结果之间的离散差异,注意这里写的是多个模型或者多次模型,即不同模型或同一模型不同时间的输出结果方差较大,方差是由训练集的数据不够导致,一方面量 (数据量) 不够,有限的数据集过度训练导致模型复杂,另一方面质(样本质量)不行,测试集中的数据分布未在训练集中,导致每次抽样训练模型时,每次模型参数不同,输出的结果都无法准确的预测出正确结果;
3、残差(噪声)
残差是指预测结果与真实值之间的差异,这么一看,和模型偏差的定义很接近,两者的区别是偏差模型拟合度不够导致,而残差是模型准确,但仍然与真实值有一定的差异,这里可以理解成噪声,噪声是随机的,意味着不可预测,而偏差不是随机产生的,可通过一定的特征工程进行预测;
如果一个模型如果出现了高偏差的话,增加训练集的数量就没有作用了。
高偏差
偏差:描述的是预测值(估计值)的期望与真实值之间的差距。偏差越大,越偏离真实数据集。

交叉验证误差Jcv
当m(训练集)很小的时候,Jtrain(θ)也很小,因为很容易就能拟合(甚至过拟合),但用这个训练好的模型在验证集上来验证,就会出现很差的效果Jcv(θ)异常的大;随着m的增大,Jtrain(θ)开始增大,Jcv(θ)开始减小;当m越来越大的时候,Jcv(θ)也越来越小,也就是说明模型的泛化程度越来越好;但随着m的增大,Jtrain(θ)也迅速增大,然后超过了最优值,虽然Jcv(θ)也在一直减少,但是始终不会达到最优状态且离最优值很远,故而出现高偏差。所以,如果一个模型如果出现了高偏差的话,增加训练集的数量就没有作用了。
高方差
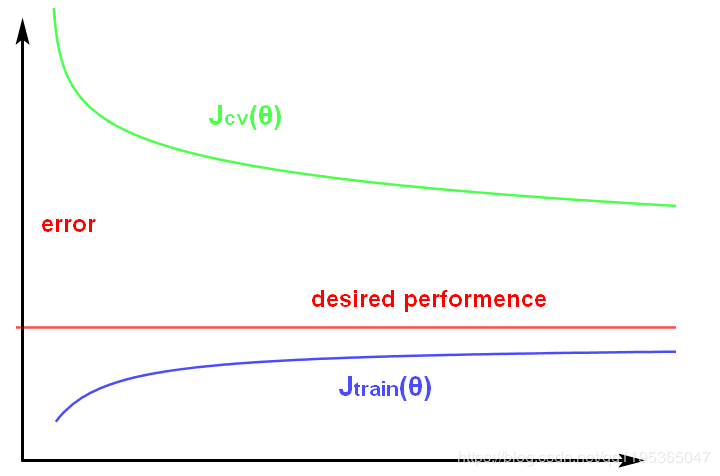
方差:描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,预测结果数据的分布越散。
当m较小时,同上面一样;随着m的增大,Jcv(θ)也逐渐变小,也就是说明模型的泛化程度越来越好;当m越来越大时,Jtrain(θ)的虽然持续在增长,但是几乎出现了停滞,很靠近最优的情况;且随着m的增长模型的泛化能力一直在增强,但同样增长得比较缓慢,故而出现了高方差。所以,如果一个模型如果出现了高方差的话,增加训练集的数量仍可以提高模型的性能。
总结
在高偏差/欠拟合的情况下,增加数据到训练集不一定能有帮助
在高方差/过拟合的情况下,增加更多数据到训练集可能可以提高算法效果
基于偏差的误差:所谓基于偏差的误差是我们模型预期的预测与我们将要预测的真实值之间的差值。偏差是用来衡量我们的模型的预测同真实值的差异。
基于方差的误差:基于方差的误差描述了一个模型对给定的数据进行预测的可变性。比如,当你多次重复构建完整模型的进程时,方差是,在预测模型的不同关系间变化的多少

左上:低偏差,低方差。表现出来就是,预测结果准确率很高,并且模型比较健壮(稳定),预测结果高度集中。
右上:低偏差,高方差。表现出来就是,预测结果准确率较高,并且模型不稳定,预测结果比较发散。
左下:高偏差,低方差。表现出来就是,预测结果准确率较低,但是模型稳定,预测结果比较集中。
右下:高偏差,高方差。表现出来就是,预测结果准确率较低,模型也不稳定,预测结果比较发散。
偏差(bias):对象是单个模型, 期望输出与真实标记的差别。
方差(Variance):对象是多个模型,表示多个模型差异程度。
版权声明:本文为CSDN博主「凯旋的皇阿玛」的原创文章,遵循CC 4.0 by-sa版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq1195365047/article/details/98442608






