在循环神经网络(RNN)模型与前向反向传播算法中，我们总结了对RNN模型做了总结。由于RNN也有梯度消失的问题，因此很难处理长序列的数据，大牛们对RNN做了改进，得到了RNN的特例LSTM（Long Short-Term Memory），它可以避免常规RNN的梯度消失，因此在工业界得到了广泛的应用。
下面我们就对LSTM模型做一个总结。
1. 从RNN到LSTM
在RNN模型里，我们讲到了RNN具有如下的结构，每个序列索引位置t都有一个隐藏状态 h(t) 。
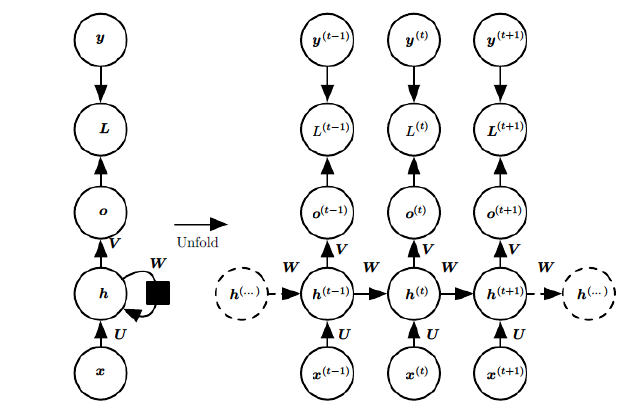
如果我们略去每层都有的 o(t) , L(t) , y(t) ，则RNN的模型可以简化成如下图的形式：
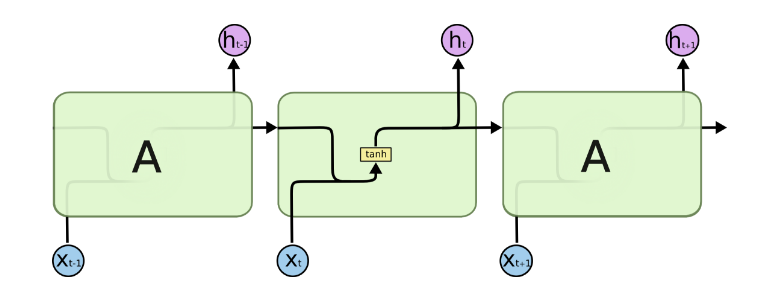
图中可以很清晰看出在隐藏状态 h(t) 由 x(t) 和 h(t−1) 得到。得到 h(t) 后一方面用于当前层的模型损失计算，另一方面用于计算下一层的 h(t+1) 。
由于RNN梯度消失的问题，大牛们对于序列索引位置 t 的隐藏结构做了改进，可以说通过一些技巧让隐藏结构复杂了起来，来避免梯度消失的问题，这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种，这里我们以最常见的LSTM为例讲述。
LSTM的结构如下图：
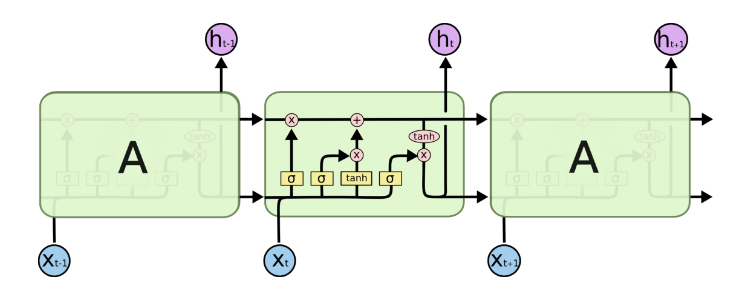
可以看到LSTM的结构要比RNN的复杂的多，真佩服牛人们怎么想出来这样的结构，然后这样居然就可以解决RNN梯度消失的问题？由于LSTM怎么可以解决梯度消失是一个比较难讲的问题，我也不是很熟悉，这里就不多说，重点回到LSTM的模型本身。
2. LSTM模型结构剖析
上面我们给出了LSTM的模型结构，下面我们就一点点的剖析LSTM模型在每个序列索引位置t时刻的内部结构。
从上图中可以看出，在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态 h(t) ，还多了另一个隐藏状态，如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State)，记为 C(t) 。
如下图所示：
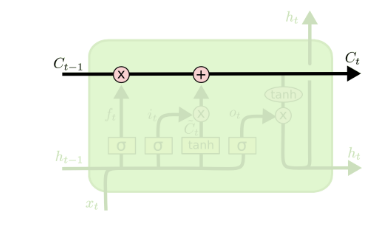
除了细胞状态，LSTM图中还有了很多奇怪的结构，这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门，输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门，输入门和输出门以及细胞状态。
2.1 LSTM之遗忘门
遗忘门（forget gate）顾名思义，是控制是否遗忘的，在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。
遗忘门子结构如下图所示：
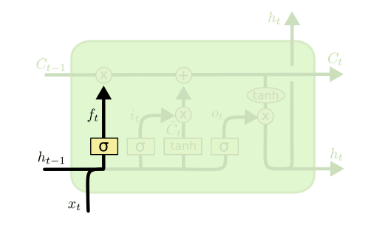
图中输入的有上一序列的隐藏状态 h(t−1) 和本序列数据 x(t) ，通过一个激活函数，一般是sigmoid，得到遗忘门的输出 f(t) 。由于sigmoid的输出 f(t) 在[0,1]之间，因此这里的输出 f^{(t)}代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为：
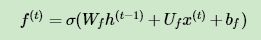
其中 Wf , Uf , bf 为线性关系的系数和偏倚，和RNN中的类似。σ为sigmoid激活函数。
2.2 LSTM之输入门
输入门（input gate）负责处理当前序列位置的输入，它的子结构如下图：
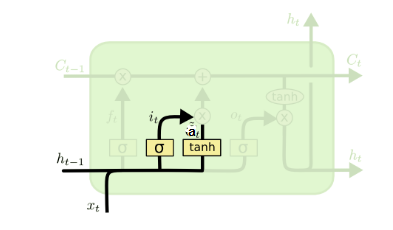
从图中可以看到输入门由两部分组成，第一部分使用了sigmoid激活函数，输出为 i(t) ，第二部分使用了tanh激活函数，输出为 a(t) ，两者的结果后面会相乘再去更新细胞状态。用数学表达式即为：
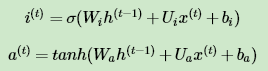
其中 Wi , Ui , bi , Wa , Ua , ba , 为线性关系的系数和偏倚，和RNN中的类似。σ为sigmoid激活函数。
2.3 LSTM之细胞状态更新
在研究LSTM输出门之前，我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态 C(t) 。我们来看看从细胞状态 C(t−1) 如何得到 C(t) 。
如下图所示：
细胞状态 C(t) 由两部分组成，第一部分是 C(t−1) 和遗忘门输出 f(t) 的乘积，第二部分是输入门的 i(t) 和 a(t) 的乘积，即：
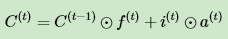
其中，⊙为Hadamard积，在DNN中也用到过。
2.4 LSTM之输出门
有了新的隐藏细胞状态 C(t) ，我们就可以来看输出门了，子结构如下：
从图中可以看出，隐藏状态 h(t) 的更新由两部分组成，第一部分是 o(t) , 它由上一序列的隐藏状态 h(t−1) 和本序列数据 x(t) ，以及激活函数sigmoid得到，第二部分由隐藏状态 C(t) 和tanh激活函数组成, 即：
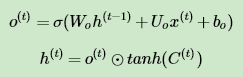
通过本节的剖析，相信大家对于LSTM的模型结构已经有了解了。当然，有些LSTM的结构和上面的LSTM图稍有不同，但是原理是完全一样的。
3. LSTM前向传播算法
现在我们来总结下LSTM前向传播算法。LSTM模型有两个隐藏状态 h(t) , C(t) ，模型参数几乎是RNN的4倍，因为现在多了 Wf , Uf , bf , Wa , Ua , ba , Wi , Ui , bi , Wo , Uo , bo 这些参数。
前向传播过程在每个序列索引位置的过程为：
1）更新遗忘门输出：
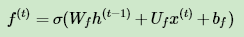
2）更新输入门两部分输出：
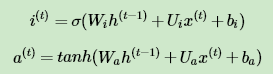
3）更新细胞状态：
4）更新输出门输出：
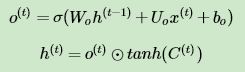
5）更新当前序列索引预测输出：
4. LSTM反向传播算法推导关键点
有了LSTM前向传播算法，推导反向传播算法就很容易了， 思路和RNN的反向传播算法思路一致，也是通过梯度下降法迭代更新我们所有的参数，关键点在于计算所有参数基于损失函数的偏导数。
在RNN中，为了反向传播误差，我们通过隐藏状态 h(t) 的梯度 δ(t) 一步步向前传播。在LSTM这里也类似。只不过我们这里有两个隐藏状态 h(t) 和 C(t) 。这里我们定义两个δ，即：
为了便于推导，我们将损失函数L(t) 分成两块，一块是时刻t位置的损失 l(t) ，另一块是时刻t之后损失 L(t+1) ，即：
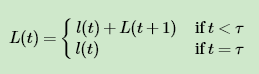
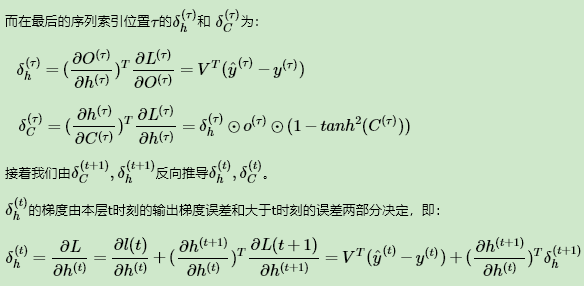
整个LSTM反向传播的难点就在于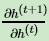
这部分的计算。仔细观察，由于 h(t) = o(t) ⊙tanh( C(t) ) , 在第一项 o(t) 中，包含一个h的递推关系，第二项 tanh( C(t) )就复杂了，tanh函数里面又可以表示成：
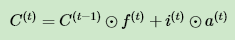
tanh 函数的第一项中，f(t) 包含一个h的递推关系，在tanh函数的第二项中，i(t) 和a(t) 都包含h的递推关系，因此，最终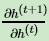这部分的计算结果由四部分组成。即：
5. LSTM小结
LSTM虽然结构复杂，但是只要理顺了里面的各个部分和之间的关系，进而理解前向反向传播算法是不难的。当然实际应用中LSTM的难点不在前向反向传播算法，这些有算法库帮你搞定，模型结构和一大堆参数的调参才是让人头痛的问题。不过，理解LSTM模型结构仍然是高效使用的前提。
参考资料：
1） Neural Networks and Deep Learning by By Michael Nielsen
2）Deep Learning, book by Ian Goodfellow, Yoshua Bengio, and Aaron Courville
3） UFLDL Tutorial
4）Understanding-LSTMs
（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）
本文转自：博客园 - 刘建平Pinard，转载此文目的在于传递更多信息，版权归原作者所有。
