卷积操作的维度计算是定义神经网络结构的重要问题,在使用如PyTorch、Tensorflow等深度学习框架搭建神经网络的时候,对每一层输入的维度和输出的维度都必须计算准确,否则容易出错,这里将详细说明相关的维度计算。
一、卷积操作的维度计算
卷积操作的维度计算是定义神经网络结构的重要问题,在使用如PyTorch、Tensorflow等深度学习框架搭建神经网络的时候,对每一层输入的维度和输出的维度都必须计算准确,否则容易出错,这里将详细说明相关的维度计算。
首先,我们看一下卷积操作涉及的东西,一个卷积操作需要定义卷积核的大小、输入图像的padding长度以及卷积操作的步长。以一个RGB图像输入为例,一个多卷积核操作的示意图如下:
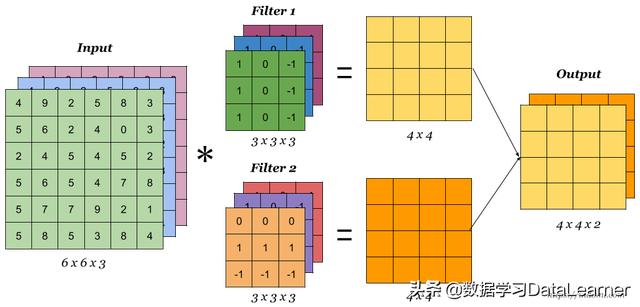
这个例子的输入数据是一个三维数据,带有通道数,输入数据第三个维度是通道数,使用了两个卷积核(滤波器)扫描得到一个带有两个通道的图像(一个卷积核对一个三维的数据,即带多个通道的二维图像扫描可以得到一个二维单通道图像结果,要求卷积核也是三维,且通道数和输入数据通道数一样)。下面我们来描述具体计算。
假设输入数据大小是w × h,其中,w是宽度,h是高度。扫描的卷积核大小是f × f。padding的长度是p(padding),步长是s(stride)。那么经过卷积操作之后,输出的数据大小:
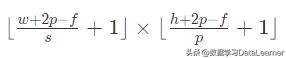
如果输入的数据是三维数据,即:w × h × c。其中,w是宽度,h是高度,c是通道数(对于RGB图像输入来说,这个值一般是3,在文本处理中,通常是不同embedding模型的个数,如采用腾讯训练的、谷歌训练的等)。这个时候的卷积核通常也是带通道的三维卷积核:f × f × c。
注意,一般来说,卷积核的通道数c和输入数据的通道数是一致的。因此,这个时候卷积之后的输出依然是一个二维数据,其大小为:
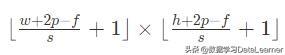
这里的维度做了向下取整,防止结果不是整数的情况。假如希望输出的也是带通道的结果,那么这时候就要使用多个卷积核来操作了,最终输出的数据维度是:
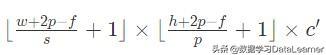
其中c'是卷积核的个数。
二、深度学习框架中Conv1d、Conv2d
在像PyTorch、Tensorflow中,都有类似Conv1d、Conv2d和Conv3d的操作。这也都和卷积操作的维度有关,里面的参数都要定义好。例如如下的卷积操作:
self.convs = nn.Sequential( nn.Conv1d(in_channels=32, out_channels=16, kernel_size=5, stride=1, padding=0), nn.BatchNorm1d(16), nn.ReLU(inplace=True) )
这里面的参数要定义好,否则容易出错。我们将分别介绍。
Conv1d是一维卷积操作,它要求输入的数据是三维的,即:N × C_in × L_in。
最终输出的参数也是三维的:N × C_out × L_out。
这里的N是mini batch size,C是通道数量,L是宽度。
这里的out_channels定义了将由几个卷积核来扫描,kernel_size则定义了每一个卷积核大小,都可以自己定义。最终,输出的min_batch_size不变,out_channels数量根据定义的参数来,而输出的width计算如下:
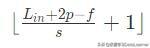
这里的p是上面padding的参数值,f是kernel_size的值。类似的,如果使用Conv2D做卷积操作,那么输入就是四维的:N × C_in × H_in × W_in。
这里的N是min batch size,C_in是输入数据的通道数,H_in是输入数据的高度,W_in是输入数据的宽度。其输出也是四维的,根据定义的卷积核大小和数量得到的输出维度如下:N × C_out × H_out × W_out。其中,C_out是根据卷积核的数量定义的输出数据的通道数,因为一个卷积核只能扫描得到一个二维图。其中H_out 和 W_out的计算如下:

三、总结
卷积操作的输入和输出数据的维度在构建神经网络中很重要,也很容易出错。使用PyTorch或者Tensoflow构建卷积神经网络的时候一定要注意参数的设置,如果计算错误,下一层的输入与上一层的输出对不上那么很有可能失败。为了避免这种情况发生,可以先用小数据集测试,同时为了检测哪里出错可以在测试的时候把每一层的输出结果的维度(shape)打印出来,这样就更容易检测结果了。
本文转自:今日头条 - 数据学习DataLearner,转载此文目的在于传递更多信息,版权归原作者所有。






