深度学习中的卷积
当提到神经网络中的卷积时,我们通常是指由多个并行卷积组成的运算。(因为单个核只能特区一种类型的特征,我们usually希望可以在多个位置提取多个特征)
输入也不仅仅是实值的网格,而是由一系列观测数据的向量构成的网格。
我们有的时候会希望跳出核中的一些位置来降低计算的开销(相应的代价是提取特征没有先前那么好了)我们就把这个过程看作对全卷积函数输出的下采样(downsampling).如果只是在输出的每个方向上每间隔s个像素进行采样,那么可重新定义一个 下采样卷积函数。我们把s称为下采样卷积的步幅(stride)。
在任何卷积网络的实现中都有一个重要性质:能够隐含地对输入V用零进行填充(pad)使得它加宽。
普遍意义的卷积
从数学上讲,卷积只不过是一种运算,对于很多没有学过信号处理,自动控制的同学来说各种专业的名词可以不做了解。我们接着继续:
本质上卷积是将二元函数 U(x,y) = f(x)g(y) 卷成一元函数 V(t) ,俗称降维打击。
怎么卷?
考虑到函数 f 和 g 应该地位平等,或者说变量 x 和 y 应该地位平等,一种可取的办法就是沿直线 x+y = t 卷起来:
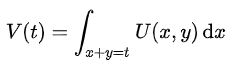
卷了有什么用?
可以用来做多位数乘法,比如:
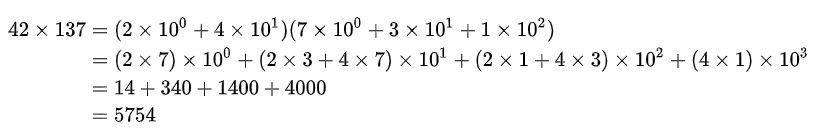
注意第二个等号右边每个括号里的系数构成的序列 (14,34,14,4),实际上就是序列 (2,4) 和 (7,3,1) 的卷积
在乘数不大时这么干显得有点蛋疼,不过要计算很长很长的两个数乘积的话,这种处理方法就能派上用场了,因为你可以用快速傅立叶变换 FFT 来得到卷积,比示例里的硬乘要快。
这里有一个不太严格的理解:
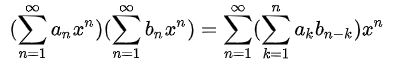
xn 是“基”,an 是在这个基上的展开系数。两个多项式乘积的在基上展开的系数就是两个多项式各自在基上展开系数的卷积。
xn 对应着频率不同的 exp(ikt) ,系数对应着其傅里叶变换。自然就是乘积的傅里叶变换等于傅里叶变换的卷积了。
本文转自:CSDN - 刺客五六柒,转载此文目的在于传递更多信息,版权归原作者所有。
原文链接:https://blog.csdn.net/qq_39521554/article/details/81635722






